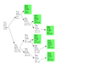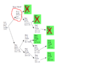- #1
fignewtons
- 28
- 0
Homework Statement
Imagine you are playing a game with me, of drawing balls from a box. There are two blue balls and two red balls. They are picked with equal probability, and are drawn without replacement. If you draw a blue ball, I give you $1. If you draw a red ball, you pay me $1.25. What is the expected value of this game to you if you are allowed to stop at any point?
Homework Equations
I drew a lattice diagram that shows the value of the game in all the possible states of the balls.
(b,r) means that at this point, there are b blue balls and r red balls.
That is, something like this:
The boxed values indicate the value at each point in time, calculated recursively.
The Attempt at a Solution
I was able to figure out the value of the game if you were required to play until the box was completely empty using a recursive method.
the expected value at any point (b,r), V(b,r) = max((b/(b+r))(1 + V(b-1, r)) + (r/(b+r))(-1.25 + V(b, r-1)),0)
where V(b,r) is the method of value of the game at the situation with b blue balls and r red balls.
So V(2,2) is the value at the beginning of the complete game, so it was 0.4583 approximately if we were required to play until all the balls had been drawn.
I'm not sure how to compute the value of the game to you if you have the option of stopping whenever you want. I was told it was (1/3) but I don't know how this number comes about. Can someone explain how the way you value the game given this option is different from the one above, and how it is calculated? Thanks.