Estimate Paint Amount for Hemispherical Dome w/ Differentials

Click For Summary
SUMMARY

This discussion focuses on estimating the amount of paint required for a hemispherical dome using differentials. The diameter of the dome is 46 meters, leading to a radius of 23 meters. The volume differential is calculated using the formula dv = 2π(23m)²(0.0003m), resulting in an estimated paint volume of 0.3174 m³, which rounds to 0.32 m³. The initial error in the calculation was due to the omission of π in the formula.

PREREQUISITES
  • Understanding of differential calculus
  • Familiarity with volume formulas for spheres and hemispheres
  • Basic knowledge of unit conversions (cm to m)
  • Proficiency in using calculators for mathematical computations
NEXT STEPS
  • Study the application of differentials in real-world scenarios
  • Learn more about volume calculations for various geometric shapes
  • Explore the use of π in mathematical equations and its significance
  • Practice problems involving differential calculus and volume estimation
USEFUL FOR

Students in calculus courses, mathematics educators, and anyone involved in practical applications of geometry and volume estimation.

Micah2
Messages
3
Reaction score
0
Use differentials to estimate the amount of paint needed to apply a coat of paint 0.03 cm thick to a hemispherical dome with diameter 46 m. (Round your answer to two decimal places.)

First I list what I am given:
Diameter: 46m
DR: 0.0003m (converted from the 0.03cm that was given)
DV: ?

Volume of a Sphere = 4/3 pi r^3
But volume of a half a Sphere = 2/3 pi r^3
And Radius = Diameter/2

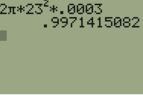
So...dv = 2 pi (23m)^2 (0.0003m)

Using a Calculator I am given 0.3174. The question asks to round it to two decimal places, which would be 0.32.
All homework is done online but apparently this answer is still incorrect. I appreciate all and any help to sort this out. :(
 
Physics news on Phys.org
you forgot the $\pi$ ...
 

Attachments

  • hemisphere_dV.png
    hemisphere_dV.png
    380 bytes · Views: 151
skeeter said:
you forgot the $\pi$ ...

Doh! Yes, that did the trick. Thank you so much! :)
 

Similar threads

MHB Estimate Paint for Hemispherical Dome - Linear Approximation
  • · Replies 1 ·
Replies
1
Views
2K
MHB *est amt of paint to a coat of paint 0.05 cm thick
  • · Replies 4 ·
Replies
4
Views
31K
MHB -z.57 dx formula that estimates the change
  • · Replies 1 ·
Replies
1
Views
7K
MHB Calculating Volume of a Hollow Sphere w/ Differentials
  • · Replies 2 ·
Replies
2
Views
2K
MHB OliverG's Calculus Q: Estimating Pool Volume w/ Trap Rule
  • · Replies 1 ·
Replies
1
Views
3K
Good ole hemispherical dome differentials problem
  • · Replies 5 ·
Replies
5
Views
11K
How Much Paint for a Hemispherical Dome Using Differentials?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Mattie_j37890's Q: Estimate Critical Values of Function
  • · Replies 1 ·
Replies
1
Views
5K
Differentials and paint needed problem
  • · Replies 7 ·
Replies
7
Views
8K
How Much Paint Is Needed for a Hemispherical Dome?
  • · Replies 6 ·
Replies
6
Views
12K