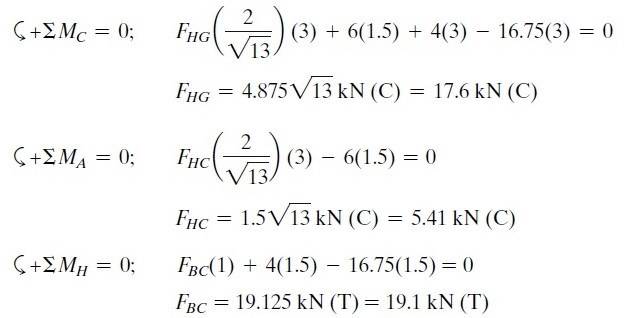Discussion Overview
The discussion revolves around the application of the method of sections to solve for forces in a truss system, specifically focusing on the calculation of moments about points A and C. Participants explore the proper distances and components to consider when analyzing forces in the truss.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant questions the use of a 3-meter distance for forces Fhc and Fhg when they believe it should be 1.5 meters, seeking clarification on which components are considered in the moment calculations.
- Another participant provides a calculation indicating that the perpendicular distance from the line of action of Fhc to point A is 1.66 meters, derived from the angle of 33.69° with respect to AC.
- There is a repeated inquiry about the rationale for using a distance of 3 meters instead of 1 meter for the vertical perpendicular distance to Fhc, emphasizing the need for clarity on this point.
- One participant argues against breaking forces into x and y components, suggesting that the forces should be considered in alignment with the links of the truss.
- Another participant mentions the necessity of considering the additional moment induced by the vertical component of Fhc when calculating the actual force.
- Links to external resources are provided for further reference on the method of sections and truss analysis.
Areas of Agreement / Disagreement
Participants express differing views on the appropriate distances and components to consider in the moment calculations, indicating that multiple competing perspectives remain unresolved.
Contextual Notes
There are unresolved assumptions regarding the definitions of distances and angles used in the calculations, as well as the appropriateness of considering force components in the analysis.