opus
Gold Member
- 717
- 131
- Homework Statement
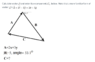
- Solve for leg C in the following picture
- Relevant Equations
- Law of Sines
Law of Cosines
So we'd like to find leg C.
But we can't use Law of Cosines yet so we will use Law of Sines.
We can easily find the length of A and this is ##\sqrt{13}##.
With some geometry we can see that ##\angle a = 53.1##.
We can now use Law of sines.
$$\frac{\sin(a)}{A} = \frac{\sin(b)}{B}$$
We want to find ##\angle b##. So we have
$$\angle b = \sin^{-1}\left(\frac{B\sin(a)}{A}\right)$$
$$\angle b = \sin^{-1}\left(\frac{5\sin(53.1)}{\sqrt{13}}\right)$$
However this gives me a domain error in my calculator which makes sense because the argument is greater than 1. It's been awhile since I've done trig, so I'm wondering how to remedy this so that I can use the Law of Cosines after this?
Thanks
But we can't use Law of Cosines yet so we will use Law of Sines.
We can easily find the length of A and this is ##\sqrt{13}##.
With some geometry we can see that ##\angle a = 53.1##.
We can now use Law of sines.
$$\frac{\sin(a)}{A} = \frac{\sin(b)}{B}$$
We want to find ##\angle b##. So we have
$$\angle b = \sin^{-1}\left(\frac{B\sin(a)}{A}\right)$$
$$\angle b = \sin^{-1}\left(\frac{5\sin(53.1)}{\sqrt{13}}\right)$$
However this gives me a domain error in my calculator which makes sense because the argument is greater than 1. It's been awhile since I've done trig, so I'm wondering how to remedy this so that I can use the Law of Cosines after this?
Thanks