Valid Estimation of Square Roots?

[clabulis]

I've been playing around with a forumlaic representation of a known square roots estimation method and I came up with this:

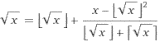
This estimation has several interesting properties to it which I've been looking into.

My main concern is the fact that I'm using SQRT(x) in the equation which is exactly what we're estimating. Obviously the exact value of SQRT(x) does not need to be known in order to perform this equation since the FLOOR and CEILING functions are being applied to it, but is this valid?

 

[rasmhop]

My main concern is the fact that I'm using SQRT(x) in the equation which is exactly what we're estimating. Obviously the exact value of SQRT(x) does not need to be known in order to perform this equation since the FLOOR and CEILING functions are being applied to it, but is this valid?

Valid according to what standards?

If you're wondering whether it's actually easier to calculate the right hand side, then the answer is yes assuming you are not completely naive (naive approach: calculate sqrt(x), then apply ceil or floor).
To calculate \lfloor \sqrt{x}\rfloor simply iterate the integers k=1,2,... until k^2 > x which gives a quick way of calculating it.

As I see it under a normal computation model your approximation takes O(sqrt(x)) time to calculate.

However there is no standard of approximation descriptions that says exactly what you're allowed to do. I consider:
\sqrt{x+1}^2
to be a perfectly valid way to approximate a positive real number x. For large x it's fairly accurate. However from a practical standpoint I probably wouldn't use it since I have access to the precise value.

 

[bndnchrs]

This is like a weight combo of up and down Bahkshali, right?Here's your relative error:

It has an exponential approach curve

I think its a smart idea but computationally its as efficient as Bahkshali... and there are more efficient methods than Bahkshali. Mathematica isn't cooperating with me to show the error for B right now. :(

 

[clabulis]

I think you might've entered the formula incorrectly into Mathematica. Here's what my relative error graphs look like. The first one shows 0<=x<=2 (when the error is at its greatest). The second one shows 0<=x<=100,000.

The formula's error approaches 0 as x approaches ∞.

In fact, here is a graph of SQRT(x) in comparison to the estimating formula:

There are some very interesting properties with this:

1.)

So this also says that the integral from [0,n] = SQRT(n)/6

2.) The largest difference for k-k_e for each interval [m,n] can be found at the point: (2SQRT(m)+1/4, 1/4(SQRT(m)+SQRT(n)))

3.) The x-value for the largest relative error in the interval [m,n] = m + SQRT(m)

Overall, the largest relative error that my formula will give on the interval [1,∞] is at x=2. The relative error at that value is approximately 0.05719

 

[bndnchrs]

Right: I just meant the ratio, not the relative error.

I just did \frac{yours}{actual}I don't understand that third statement: the largest error in [m,n] is at m + sqrt(m)? This isn't always in the interval. I'm also not sure what you mean by 2) your largest error is at two points? The error is definitely "parabolic" between zeros, so only one max: and 2*sqrt(m) + 1/4 is always less than m for m > 4, so its not in the interval. Likewise unless n is large enough the second value isn't in there.

 

[Hurkyl]

For the record, your formula looks very much like one iteration of Newton's method for approximating a root of

f(y) = y² - x​

 

[bndnchrs]

right, just approximating x by floors and ceilings

 

[D H]

For the record, your formula looks very much like one iteration of Newton's method for approximating a root of

f(y) = y² - x​

Almost, but this new expression is less accurate and is more complex computationally.

It would be even more like one iteration of that method by using only floor rather than floor and ceiling in the denominator of the second term:

\sqrt x \approx \lfloor \sqrt x \rfloor +<br /> \frac{a - \lfloor \sqrt x \rfloor^2}{2\lfloor \sqrt x \rfloor}

This is more accurate than the floor+ceiling method. It is in fact the first iteration of Newton's method starting with an initial guess of \lfloor \sqrt x\rfloor.

Except it still has a higher computational cost compared to Newton's method.