SUMMARY
The discussion clarifies the distinction between vector fields and differential forms, emphasizing their dual nature in mathematics. It asserts that the expression \frac { \partial } { \partial u } is not a vector field and corrects a misinterpretation of the expression \frac { \partial } { \partial u } = \frac { \partial u } { \partial x } \frac { \partial } { \partial x } + \frac { \partial u } { \partial y } \frac { \partial } { \partial y }. The correct formulation is \frac { \partial } { \partial u } = \frac { \partial x } { \partial u } \frac { \partial } { \partial x } + \frac { \partial y } { \partial u } \frac { \partial } { \partial y }, where x and y are functions of u and v.
PREREQUISITES
- Understanding of vector fields and differential forms
- Familiarity with partial derivatives
- Knowledge of multivariable calculus
- Basic concepts of dual spaces in mathematics
NEXT STEPS
- Study the properties of differential forms in advanced calculus
- Learn about the applications of vector fields in physics
- Explore the concept of dual spaces in linear algebra
- Investigate the relationship between partial derivatives and coordinate transformations
USEFUL FOR
Mathematicians, physics students, and anyone studying advanced calculus or differential geometry will benefit from this discussion.
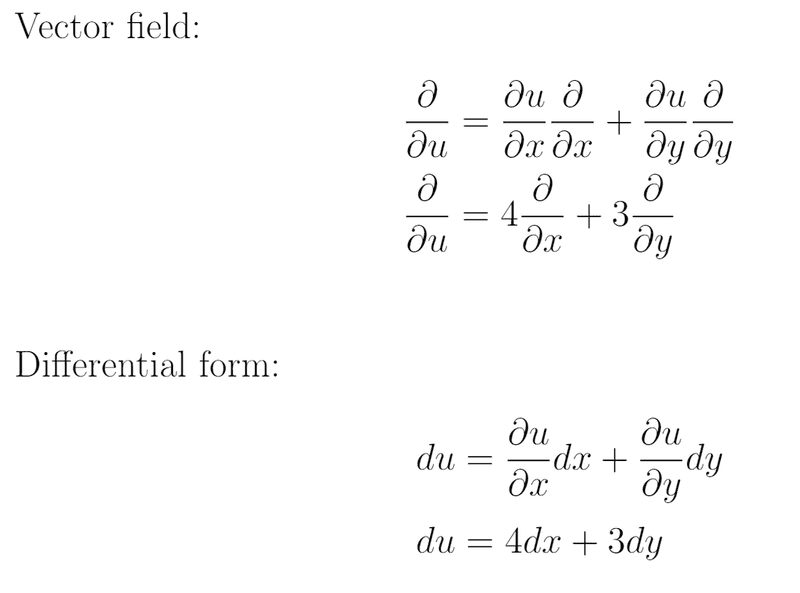 So my question is: Are these right and how do they differ from each other?
So my question is: Are these right and how do they differ from each other?