Vector Laplacian: different results in different coordinates

[maajdl]

Hello,

I calculated the Vector Laplacian of a uniform vector field in Cartesian and in Cylindrical coordinates.
I found different results.
I can't see why.

In Cartesian coordinates the vector field is: (vx,vy,vz)=(1,0,0).
Its Laplacian is: (0,0,0) .
That's the result I expected.

In Cylindral coordinates the same vector field becomes: (vr,vt,vz)=(cos(t),sin(t),0).
I found its Laplacian to be: (-4cos(t)/r²,-4sin(t)/r²,0) .

I used Mathematica to calculate this, using the definition for 3D space:

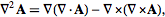
I expected the result would not depend on the choice of the coordinate system.
I also expected the result would be (0,0,0) in any coordinate system.

My motivation was to understand the meaning of a v/r² term appearing in the Laplacian in cylindrical coordinates.
I hoped that probing with a uniform field would help to reveal the meaning.

Would you have a clue?

Thanks,

Michel

 

[maajdl]

Additional comment:

The same problem in 2 dimensions (either Cartesian or Polar coordinates) leads to no contradiction.
This is because the sign before the curl operator in the definition of the Vector Laplacian must be changed to positive in 2D.
In that case, the Laplacian of the above uniform field is indeed (0,0) in both coordinate systems.

 

[maajdl]

Sorry!
Just realized my mistake.
The vector field in cylindrical coordinates should read: (vr,vt,vz)=(cos(t),-sin(t),0) .
Then it fits.

 

[jedishrfu]

It's really great that as you describe the problem, the mistake becomes obvious and new insight is gained.

I think this is one motivation for teachers, that as you explain things to students you realize the many assumptions that you have made when you first learned it and your struggle to explain the assumptions forces or inspires you to a new insight.