Vector Laplacian: Scalar or Vector?

[olgerm]

according to this page https://en.wikipedia.org/wiki/Vector_Laplacian value of Vector_Laplacian is vector, but according to this page https://en.wikipedia.org/wiki/D'Alembertian value of Vector_Laplacian is scalar

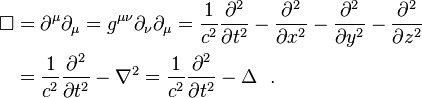
Is on of these pages wrong or I misunderstand it?

I am asking because I want to know what does Δ² equal to in this

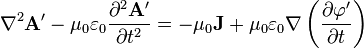and this

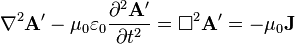equation on this https://en.wikipedia.org/wiki/Mathematical_descriptions_of_the_electromagnetic_field#Coulomb_gauge page.

 

[Orodruin]

The d'Alembertian is a differential operator. You can apply it to a scalar and get a scalar, or you can apply it to a vector and get a vector.

 

[olgerm]

So since magnetic potential A in this equation

is vector $\nabla^2=(\sum_{i=1}^3(\frac{\partial^2 A}{\partial x_i*\partial x_1});\sum_{i=1}^3(\frac{\partial^2 A}{\partial x_i*\partial x_2});\sum_{i=1}^3(\frac{\partial^2 A}{\partial x_i*\partial x_3}))$ not $\nabla^2=\sum_{i=1}^3(\frac{\partial^2 A}{\partial x_i^2})$?
These are Cartesian coordinates.

 

[Orodruin]

It is unclear what you intend to write with these expressions. In particular, it is unclear what you intend for $A$ to be (the vector, the vector components, etc). I strongly suggest that you do not write vectors on component form (x;y;z), but instead use basis vectors. This will make it much clearer what is intended.

The Laplace operator applied to a vector in Cartesian coordinates is such that the $x$ component of $\nabla^2 \vec A$ is equal to $\nabla^2 A_x$, where $A_x$ is the $x$ component of $\vec A$.

 

[olgerm]

A is vector-field. I am trying to find out what does $\nabla^2 A$, on this Wikipedia page
https://en.wikipedia.org/wiki/Mathematical_descriptions_of_the_electromagnetic_field#Gauge_freedom , equal to.
Is it that $(\nabla^2 A)_j=\sum_{i=1}^3(\frac{\partial^2 A_j}{\partial x_i^2})$?
Where $A_i$ is the $i$ component of $\vec A$.

 

[Orodruin]

A is vector-field. I am trying to find out what does $\nabla^2 A$, on this Wikipedia page
https://en.wikipedia.org/wiki/Mathematical_descriptions_of_the_electromagnetic_field#Gauge_freedom , equal to.
Is it that $(\nabla^2 A)_i=\frac{\partial^2 A_i}{\partial x_i^2}$ or $(\nabla^2 A)_j=\sum_{i=1}^3(\frac{\partial^2 A_i}{\partial x_i \cdot \partial x_j})$ or $\nabla^2 A=\sum_{i=1}^3(\frac{\partial^2 A_i}{\partial x_i^2})$?
Where $A_i$ is the $i$ component of $\vec A$.

Neither, see my previous post.

Your first option is just one term in the sum, your second is grad(div(A)) and not the Laplacian of A, your third is a scalar.

 

[olgerm]

So on this Wikipedia page
https://en.wikipedia.org/wiki/Mathematical_descriptions_of_the_electromagnetic_field#Gauge_freedom $(\nabla^2 A)_j=\sum_{i=1}^3(\frac{\partial^2 A_j}{\partial x_i^2})$?

 

[Orodruin]

So on this Wikipedia page
https://en.wikipedia.org/wiki/Mathematical_descriptions_of_the_electromagnetic_field#Gauge_freedom $(\nabla^2 A)_j=\sum_{i=1}^3(\frac{\partial^2 A_j}{\partial x_i^2})$?

Yes. Although this is only valid in Cartesian coordinates.

 

[olgerm]

Yes. Although this is only valid in Cartesian coordinates.

Ok, thanks.