Velocity of a falling folded rope and reaction force

[Raphael30]

Homework Statement

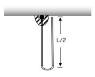
A rope of length L and mass m is attached to the ceiling and folded at mid length. The free end of the rope is held against the ceiling, then dropped at time t=0.

a) Calculate the velocity of the free end as a function of y, its distance from the ceiling.
b) Calculate R, the reaction force exerted by the ceiling as a function of y.

Homework Equations

Free fall: a=g, v=gt, y=0.5gt^2, therefore v^2=2gy; R=-Fg

The Attempt at a Solution

[/B]
I couldn't find a way the free end was subject to any rope tension, so I supposed its fall was free, therefore v=sqrt(2gy)
However, at y=L, v has to become 0 because the rope is extensible.
Following the logic that the folded part didn't pull on the rope, I interpreted the reaction force as the tension in the rope, of magnitude mg/2 at the start and gaining mgy/2L as the free end drops (because the folded part loses y/2 in legth as it drops)
The goal of this exercise is supposed to be an introduction to whip dynamics, but I feel like my results are far too simple and don't really enlighten me on that subject. Can anyone verify my results and point out the flaws in my logic?

 

[Orodruin]

The tension in the rope is not given by only the force required to hold the rope up. In order for the parts of the falling rope to stop, you need to act upon it by a force. This will give a non-zero contribution to the reaction force.

 

[Raphael30]

Ok so my idea is F=dp/dt=(dp/dy)(dy/dt)
dy/dt=v=(2yg)^1/2
dp=dm x v=(my/2L)(2gy)^1/2dy
therefore F=(my/2L)(2yg)^1/2(2gy)^1/2=gmy²/L
where R=Fg+F=(mg/2L)(L+y+2y²) until y=L, where R falls to Fg=mg
I think this makes sense, doesn't it?

 

[Delta2]

I think you have a small mistake regarding $dm$, i believe we can agree that the mass of the stationary part of the rope is increasing according to

$m(y)=\frac{m}{2}(1+\frac{y}{L})$ hence
$\frac{dm}{dy}=\frac{m}{2}\frac{1}{L}\Rightarrow dm=\frac{m}{2}\frac{dy}{L}$

 

[Raphael30]

Yes, I noticed that didn't work. Also, dp/dy doesn't equal vdm/dy, dp/dy=vdm/dy+m(y)dv/dy. This doesn't affect the end result, dp/dy now simply incorporates Fg. The end result should therefore be R=dp/dt=(mg/2)(1+3y/L) until y=L, where R falls from 2mg to Fg=mg.

 

[Delta2]

Well to be honest, something puzzles me, how to explain the discontinuity at the time when y=L that R falls from 2mg to mg...
We must have done something wrong, at y=L the equation should give R(L)=mg...

 

[Delta2]

i think the correct equation is $\sum \vec{F_{external}}=\frac{d\vec{p}}{dt}\Rightarrow \vec{R}+\vec{B}=\frac{d\vec{p}}{dt} (1)$.

Also we should take as $m(y)=\frac{m}{2}(1-\frac{y}{L})$ which gives the mass of the moving part.

Then $\vec{p}=m(y)\vec{v(y)}$ and if we take as positive the direction of the weight B, then (1) becomes

$mg-R=\frac{d m(y)v(y)}{dt}$ which i believe should give the correct expression for R after we workout the details...

 

[Raphael30]

What do B and R stand for here?

 

[Delta2]

R is the force on the rope from the ceiling, and B is the weight of the rope.

 

[Raphael30]

I don't see the the difference with the way we previously solved it. The only possible mistake I could see at this point, which would make sense, is the hypothesis that the free end is free falling, which gave us the expression for v(y). If v(y) didn't drop at 0 suddenly when y=L, neither would half or our dp/dt equation. Then again, because the event of a perfectly folded rope is unrealistic, this kinda makes sense (it would end more smoothly if we took into account the curve of the fold) and would explain why whips tend to act crazy right when they're fully extended.

 

[TSny]

It's not always clear what assumptions to make in a problem like this. For this problem, there is experimental evidence that mechanical energy is conserved to a fair approximation (for most of the fall, anyway).

For example, see the first couple of paragraphs in this paper:
https://arxiv.org/pdf/physics/0508005.pdf

So, you might want to switch to the assumption that mechanical energy is conserved during the fall. In this case, the falling end does not fall freely. You'll find interesting behavior, especially near the end of the fall. In the above link, the analysis uses a Lagrangian approach. But that is not necessary.