Velocity of Buoyant Plug in Closed Loop

[erobz]

A problem I was thinking about when talking about natural circulation in a closed loop in another thread:

What is the velocity of the buoyant plug? The loop is filled with water. There are no viscous forces acting on the plug or in the flow. The flow is assumed incompressible.

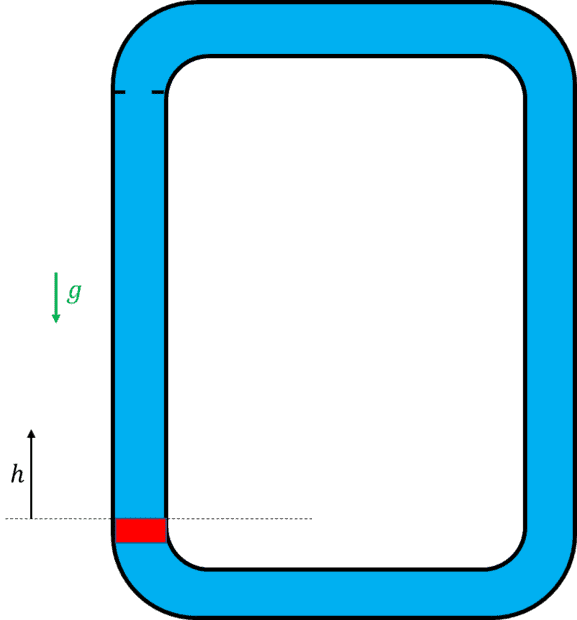
1) Is the buoyant force constant? I was thinking conservation of energy, but does the fact that the fluid is accelerating with the plug effect it?

$$ \int F_b ~dh = m_p g h + \frac{1}{2}m_p v_p^2 + \frac{1}{2}m_w v_p^2$$

with $v_w = v_p$
2) I assume its ok to neglect the small change in the fluid center of mass as the plug ascends?

 

[jbriggs444]

1) Is the buoyant force constant? I was thinking conservation of energy, but does the fact that the fluid is accelerating with the plug effect it?

The acceleration of the fluid and of the plug should be equal and constant. The net force on the plug should also be constant. Those conditions are all consistent with one another.

2) I assume its ok to neglect the small change in the fluid center of mass as the plug ascends?

One can account for the energy balance either by considering the work done by the buoyant force on the plug or by considering the potential energy of the system. Both account for both plug and fluid. Accordingly, both should yield an identical result.

One way to attack the problem is an approach based on momentum. You have a mass of fluid and a mass of plug both accelerating identically under a constant force. This is a simple SUVAT setup:$$a=f/m$$ $$v=at$$Another way is an approach based on energy. You write down an energy balance for potential and kinetic energy with kinetic energy as a function of velocity and potential energy as a function of position.$$KE + PE = C$$ $$\frac{1}{2}m_1v^2 + gm_2s = C$$Here $m_1$ is the total mass of fluid plus plug and $m_2$ is the net mass of the plug after subtracting out buoyancy. $s$ is vertical displacement, of course. Looking at this equation from a different point of view, it is just a work-energy relationship. It is the very familiar work energy relationship that is associated with a mass being accelerated under a constant force.

 

[Lnewqban]

Isn't this similar to a balance with different weights at both ends, naturally seeking a balance state?
You could replace the piston with a few drops of oil or a big bubble of air, I believe.

 

[erobz]

My concern was for the acceleration of the fluid effecting the buoyant force. For instance a submerged buoyant body looses its buoyancy when the fluid it's inside experiences freefall?

 

[jbriggs444]

My concern was for the acceleration of the fluid effecting the buoyant force. For instance a submerged buoyant body looses its buoyancy when the fluid it's inside experiences freefall?

Without calculation, I am going to trust my intuition on this one. The force on the plug is reduced by the acceleration. But this has no effect on the calculated result. In particular, you get the correct computed acceleration by dividing the "unaccelerated" buoyant force by the total mass of plug plus fluid even though that is not the actual net buoyant force applied on the accelerating plug.

How could the actual buoyant force on the accelerating plug be anything remotely close to the net force accelerating the fluid plus plug?! The net force (buoyancy minus gravity) on the plug has to be enough to accelerate the plug alone. It would not be anywhere near the right figure to account for the motion of plug plus fluid.

 

[gmax137]

What is the velocity of the buoyant plug?

I'm confused, what is this "plug?" At first I thought you meant a small control mass of the fluid, but it seems you're considering an actual solid plug? That slides axially along the pipe?

Sorry if I'm being dense. It happens.

 

[erobz]

I'm confused, what is this "plug?" At first I thought you meant a small control mass of the fluid, but it seems you're considering an actual solid plug? That slides axially along the pipe?

Sorry if I'm being dense. It happens.

I'm thinking about a solid plug of some low-density material as a first go. It slides up the tube, circulating the water in the loop.

 

[erobz]

Without calculation, I am going to trust my intuition on this one. The force on the plug is reduced by the acceleration. But this has no effect on the calculated result. In particular, you get the correct computed acceleration by dividing the "unaccelerated" buoyant force by the total mass of plug plus fluid even though that is not the actual net buoyant force applied on the accelerating plug.

How could the actual buoyant force on the accelerating plug be anything remotely close to the net force accelerating the fluid plus plug?! The net force (buoyancy minus gravity) on the plug has to be enough to accelerate the plug alone. It would not be anywhere near the right figure to account for the motion of plug plus fluid.

I'm thinking it could be a small correction, if any.... If the fluid is static, it has the hydrostatic pressure gradient across the plugs height. I was just curious how that changes given the fluid (the plug is in) is accelerating upwards. I'm not saying your intuition is wrong, I just wan't to understand if there is potential adjustment.

 

[jbriggs444]

I'm thinking it could be a small correction, if any.... If the fluid is static, it has the hydrostatic pressure gradient across the plugs height. I was just curious how that changes given the fluid the plug is in is accelerating upwards. I'm not saying your intuition is wrong, I just wan't to understand if there is potential adjustment.

The pressure field in the accelerating fluid is not the same as one would expect for a simple vertical column of accelerating fluid. It is a [nearly] closed loop. The pressure gradient around the closed loop has to add to zero.

We know how much potential energy it takes to change the position of the fluid+plug system by a certain displacement. That tells us the "force" that is causing the circulation. We know the mass of the fluid+plug system. That's it -- the calculation is essentially done at that point.

The intuitive part is that the "force" calculated for this is identical to the buoyant force on a stationary plug in a bath of the fluid at equilibrium.