SUMMARY
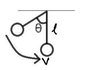
The discussion focuses on the relationship between a pendulum bob's speed and its displacement angle, specifically demonstrating that the speed at the equilibrium position is given by the formula ##v = \sqrt{2gl(1-cos\theta)}##, where ##l## is the pendulum's length. Participants emphasized the application of the conservation of energy principle, identifying the initial and final kinetic and potential energies. The height of the bob above the lowest point is derived as ##h = l(1-cos\theta)##, leading to the correct expression for speed. A final correction was made to ensure the formula was accurately presented.
PREREQUISITES
- Understanding of basic physics concepts such as kinetic energy (K.E) and potential energy (P.E).
- Familiarity with the law of conservation of energy.
- Knowledge of trigonometric functions, particularly cosine.
- Ability to interpret and analyze diagrams related to pendulum motion.
NEXT STEPS
- Study the principles of conservation of mechanical energy in oscillatory systems.
- Learn about the derivation of equations of motion for simple pendulums.
- Explore the effects of varying displacement angles on pendulum dynamics.
- Investigate the role of gravitational acceleration (g) in pendulum motion.
USEFUL FOR
Students studying physics, educators teaching mechanics, and anyone interested in understanding the dynamics of pendulum motion and energy conservation principles.