Discussion Overview
The discussion centers around the concept of velocity through spacetime, particularly whether it is always equal to 'c'. Participants explore the implications of this idea through spacetime diagrams, the nature of four-velocity, and the relationship between spatial and temporal components of motion. The scope includes theoretical considerations, mathematical reasoning, and conceptual clarifications.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
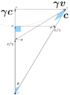
- Some participants assert that the velocity of a body through spacetime is equal to 'c', questioning whether this can be represented in a spacetime velocity diagram.
- Others argue that while 'c' represents the length of the four-velocity vector, the spatial velocity 'v' cannot be directly related to 'c' in a simple triangle diagram.
- A participant introduces a spacetime diagram using trigonometric relationships, discussing rapidity and its implications for understanding velocity in spacetime.
- Some express skepticism about the phrase "speed through time," suggesting it may be misleading or overly simplistic.
- There are discussions about the nature of four-velocity, with some participants suggesting it may be a misnomer and better understood as an extension of a unit direction vector rather than traditional velocity.
- Participants highlight the potential confusion arising from popular science descriptions of spacetime velocity, questioning their accuracy and clarity.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the interpretation of velocity through spacetime or the validity of popular science descriptions. Multiple competing views remain regarding the nature of four-velocity and its representation in diagrams.
Contextual Notes
Some participants note limitations in the popular science explanations and the potential for misinterpretation of terms like "speed through time." The discussion also reflects on the mathematical relationships between spatial and temporal components without resolving the underlying complexities.