Help Me Determine Validity of Time Dilation Formula

[diazdaiz]

TL;DR Summary

Help me determine whether this proof of time dilation formula is valid based on my understanding on ScienceClic's video

I recently trying to learn General Relativity by first scraping the surface on ScienceClic's general relativity playlist, and then I stumbled upon a video where it said that we actually move through spacetime on a constant speed of c, and then I remember about time dilation because how speed on space affect speed on time, here's my attempt on the derivation

We usually write velocity Magnitude as shown below, where Vs is V through space

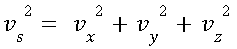
In this video

at time stamp 1:11, they said we are all moving at a constant speed of light (c) in a spacetime coordinate. Where Vst is V through spacetime and Vt is V through time:

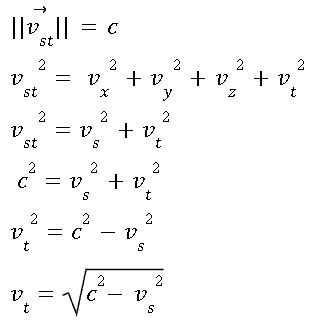
On our frame of reference, we don’t move through space is it not(?), only through time, so

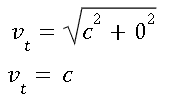
When we see other frame of reference move through space, let say Vs’, we should see him move through time slower when compared to our frame of reference

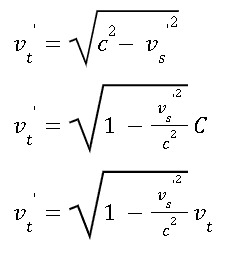
is this kind of formula derivation valid?

 

[PeterDonis]

we actually move through spacetime on a constant speed of c

This is a common pop science factoid but it does not actually have any of the implications that pop science factoid purveyors like to claim.

here's my attempt on the derivation

"Deriving" the factoid is very simple: the invariant length of any timelike object's 4-velocity vector is $c$. This is true by definition of 4-velocity. QED.

is this kind of formula derivation valid?

No. Spacetime is not Euclidean, and the 4-velocity vector is not a Euclidean vector whose squared magnitude is the sum of the squares of the components, as you are assuming.

 

[Dale]

This is a common pop science factoid but it does not actually have any of the implications that pop science factoid purveyors like to claim.

They also tend to avoid mentioning that this fact also implies that light moves through spacetime at a constant speed of 0.

 

[Ibix]

The problem is that spacetime is not Euclidean, so writing $c^2= v_t^2+v_s^2$ is not valid.

In fact, $c^2=c^2(dt/d\tau)^2-(dx/d\tau)^2$. You haven't formally defined the term $v_t$, but I suspect you mean $v_t=c(dt/d\tau)$, and for $v_s$ you seem to mean $dx/dt$. The time dilation factor you are looking for is $\gamma=dt/d\tau$ (edit: and not the other way up, as I originally wrote), and recall that $dx/dt=(dx/d\tau)(d\tau/dt)$. I'm not sure if this really counts as a derivation, since we're assuming quite a lot, but you can certainly get to $\gamma$ this way.

 

[PeterDonis]

The time dilation factor you are looking for is $\gamma=d\tau/dt$

$\gamma$ is $dt / d\tau$, not $d\tau / dt$. The components of the 4-velocity (in the units we are using, where we do not take $c = 1$, and assuming we want all the components to have the same units) are $\gamma \left( c, v_x, v_y, v_z \right)$.

 

[Ibix]

$\gamma$ is $dt / d\tau$, not $d\tau / dt$.

Aargh! It's been a long day. Corrected above - thanks.

 

[vanhees71]

They also tend to avoid mentioning that this fact also implies that light moves through spacetime at a constant speed of 0.

No, for "light" ("naive photons" aka "massless particles") there's no proper time and the definition of "four velocity" as used for massive particles is impossible.

Nevertheless the world line of such a "fictitious massless particle" is lightlike. To describe it you have to introduce an arbitrary world-line parameter. Then for the worldline you have of course
$$\dot{x}(\lambda) \cdot \dot{x}(\lambda)=0$$
along the world line.

In connection with light one should keep in mind that this idea of describing light as the motion of a massless particle refers to the geometric-optic approximation of Maxwell's equations, i.e., the eikonal approximation for em. waves. The above "trajectories" are to interpreted as the characteristics of the eikonal equation,
$$g^{\mu \nu} (\partial_{\mu} \psi \partial_{\nu} \psi)=0.$$

This implies that to set the physical scale of the affine parameter $\lambda$ for the light-like trajectory you may interpret $\dot{x}(\lambda)=k$, i.e., the wave fourvector, $(\omega/c,\vec{k})$.

The "trajectory" of the light-like particle, defined by the null-geodesic equations thus describes how the wave-fourvector of an electromagnetic wave changes from one point in spacetime to another.

 

[Nugatory]

No, for "light" ("naive photons" aka "massless particles") there's no proper time and the definition of "four velocity" as used for massive particles is impossible.

I think that’s pretty much @Dale’s point: if we use that “moving through time” model from the original post we are forced to infer a zero speed of light from the zero length of lightlike paths. This difficulty, conveniently ignored by that bogus model, is another reason to reject it.

 

[A.T.]

... that we actually move through spacetime on a constant speed of c...

Yes, but it confuses people, when you use "t" like that because it usually denotes "coordinate time". But in your case you actually mean "proper time", which is usually denoted by "τ" (tau).

This approach was used in this book (scroll the linked page down for PDF download):
https://archive.org/details/L.EpsteinRelativityVisualizedelemTxt1994Insight/mode/2up

Here a recent paper relating this geometric interpretation to the more standard one:
https://link.springer.com/article/10.1007/s10714-020-02736-5
Free version: https://arxiv.org/pdf/2004.10505.pdf

 

[vanhees71]

I think that’s pretty much @Dale’s point: if we use that “moving through time” model from the original post we are forced to infer a zero speed of light from the zero length of lightlike paths. This difficulty, conveniently ignored by that bogus model, is another reason to reject it.

Well, nevertheless although "massless particles" are fictitious they can be formaly described by null trajectories in phase space. The only thing different from massive particles is that there's no physical scale in the problem and that's why there's no "preferred affine parameter" like proper time for massive particles.

The fictitious massless particles which are often called "photons" and used particularly in GR to calculate the propagation of electromagnetic waves in given spacetimes (like the Schwarzschild spacetime to calculate the gravitational red shift on Earth and the deflection of light on the Sun or FLRW spacetime to calculate the Hubble-Lemaitre red shift of the light from far distant objects) have to be reinterpreted properly as the solution of Maxwell's equations in the given spacetime in the eikonal approximation. Then the scale is set by the frequency (at the source or the receiver) and the "worldline of the photons" describes how the wave vector of an em. "plane wave" behaves, including all the various effects like gravitational redshift and Doppler effect, gravitational deflection of light, and aberration.

 

[PeterDonis]

although "massless particles" are fictitious they can be formaly described by null trajectories in phase space.

I think you mean null trajectories in spacetime?

 

[Dale]

No, for "light" ("naive photons" aka "massless particles") there's no proper time and the definition of "four velocity" as used for massive particles is impossible.

There is still a tangent vector to a null worldline, and its "length" is null.

 

[robphy]

No, for "light" ("naive photons" aka "massless particles") there's no proper time and the definition of "four velocity" as used for massive particles is impossible.

Nevertheless the world line of such a "fictitious massless particle" is lightlike.

There is still a tangent vector to a null worldline, and its "length" is null.

In many particle physics calculations, we model a photon with a 4-momentum (which is of course null).
With that photon 4-momentum, we use conservation of total 4-momenta
to work out the Compton Effect, neutral pion decay, etc...

 

[Ibix]

Yes, but it confuses people, when you use "t" like that because it usually denotes "coordinate time". But in your case you actually mean "proper time", which is usually denoted by "τ" (tau).

I think you're arguing for the equation $v_{st}^2=v_s^2+v_t^2$ to be interpreted as meaning that $v_t^2$ is the modulus squared of a four vector $(v_{st},\vec v_s)$, and choosing normalisation such that the first component is $c$ in our frame of choice. Then I think that $v_s$ is the "proper speed" (aka celerity) and $v_t=c/\gamma$.

I'd agree that works, and it isn't an interpretation that had occurred to me. But I think that you need a fairly creative reading of what the OP wrote to say that's what he was trying to do.

 

[robphy]

In some approaches to relativity (like this and like the Loedel and Brehme approaches [which also try to use "Euclidean" calculations]), one is able to obtain the various textbook formulas for these simple cases.
But I wonder if these techniques apply as well to more complicated problems.

If the goal is just to scrape the surface of relativity, then such methods may be okay.
But for a deeper understanding, I suspect these methods (ok, I'll say it: "tricks") won't get you there.
Minkowski spacetime geometry, suitably generalized to pseudo-Riemannian geometry, can get you there.

(From my study of the Loedel diagram, it already has trouble with the Clock Effect with unequal outgoing and return velocities. The method needs to "boost" into convenient frames to different parts of a calculation.
It's like doing Euclidean geometry where we have always rotate a feature into "standard form" before we can work on it... then rotate back to interpret it in the original frame.)

(By the way, I hate algebraic solutions to relativity problems that involve boosting into a frame, then boosting back. There is almost certainly a geometric or trigonometric solution, which recalls a similar construction from Euclidean geometry... possibly giving some intuition to the situation.)

My $0.02.

 

[PeterDonis]

I think you're arguing for the equation $v_{st}^2=v_s^2+v_t^2$ to be interpreted as meaning that $v_t^2$ is the modulus squared of a four vector $(v_{st},\vec v_s)$, and choosing normalisation such that the first component is $c$ in our frame of choice.

This is not the usual normalization, though. In the usual normalization, the invariant length of the 4-velocity is $c$, and the components are $(\gamma c, \gamma \vec{v})$.

Then I think that $v_s$ is the "proper speed" (aka celerity) and $v_t=c/\gamma$.

Not with the normalization you gave. Celerity is $\gamma \vec{v}$, where $\vec{v}$ is the ordinary velocity. But that requires the first component to be $\gamma c$, not just $c$.

 

[Ibix]

This is not the usual normalization, though. In the usual normalization, the invariant length of the 4-velocity is $c$, and the components are $(\gamma c, \gamma \vec{v})$.

Quite. That's part of why I said I thought it was a creative interpretation, since the video seems to be using the usual four velocity normalisation.

Not with the normalization you gave. Celerity is $\gamma \vec{v}$, where $\vec{v}$ is the ordinary velocity. But that requires the first component to be $\gamma c$, not just $c$.

Ugh. I wonder how many more $\gamma$ factor errors I can make. Then $v_s$ is the usual three velocity ("velocity through space") in this interpretation, at least in the chosen frame in which the "velocity through time" is $c$.

 

[PeterDonis]

Then $v_s$ is the usual three velocity ("velocity through space") in this interpretation, at least in the chosen frame in which the "velocity through time" is $c$.

Even that doesn't work. The fundamental problem is that the 4-vector components are the ones the metric applies to. If you divide out $\gamma$ from the components you no longer have a 4-vector; $(c, \vec{v})$ does not transform correctly. You can call $\vec{v}$ a "3-velocity", but you can't interpret it as the "space part" of a 4-vector of which $c$ is the "time part".

 

[Ibix]

Even that doesn't work. The fundamental problem is that the 4-vector components are the ones the metric applies to. If you divide out $\gamma$ from the components you no longer have a 4-vector; $(c, \vec{v})$ does not transform correctly. You can call $\vec{v}$ a "3-velocity", but you can't interpret it as the "space part" of a 4-vector of which $c$ is the "time part".

It works as long as you interpret it the way I originally said, as a four vector normalised so that the time component is $c$ in our chosen frame. The $\gamma$ is the Lorentz gamma in that same frame, and the four vector is a legitimate four vector parallel to the four velocity. Its modulus only has an interpretation in terms of the object's gamma in the original frame, but similar statements apply to the components too.

I don't like this particularly, but I think it works, albeit in a rather contrived way. Maybe A.T. didn't have a four vector in mind and was just relating frame dependent quantities in a way that can be interpreted as a rather odd four vector.

 

[A.T.]

But I think that you need a fairly creative reading of what the OP wrote to say that's what he was trying to do.

I misread the OPs formula based on the OPs introductory comment. I fixed the quote to indicate what I was referring too.

 

[PeterDonis]

It works as long as you interpret it the way I originally said, as a four vector normalised so that the time component is $c$ in our chosen frame.

If you do this, then the space component will only be $\vec{v}$ in that chosen frame as well; when you transform it to another frame, the space component won't be the 3-velocity in that other frame. But the whole point of the "moving through spacetime at $c$" interpretation is that it should be true in every frame. And the only way that works is with the standard normalization of the 4-velocity. (Note that, as stated in the OP, it's moving through spacetime at $c$, not moving through time at $c$.)

 

[robphy]

Even that doesn't work. The fundamental problem is that the 4-vector components are the ones the metric applies to. If you divide out $\gamma$ from the components you no longer have a 4-vector; $(c, \vec{v})$ does not transform correctly. You can call $\vec{v}$ a "3-velocity", but you can't interpret it as the "space part" of a 4-vector of which $c$ is the "time part".

Slightly off-topic:

Let me point out that there is, unfortunately, a textbook that uses this
https://books.google.com/books?id=UMDurS6HSl4C&q=4-velocity#v=snippet&q=4-velocity&f=false

The Geometry of Spacetime: An Introduction to Special and General Relativity
By James J. Callahan

Later, he introduces a "proper 4-velocity" (which may be related to the use
of https://en.wikipedia.org/wiki/Proper_velocity (celerity) as the space-component of
this [Callahan-proper] 4-velocity . Note the use of relativistic-mass below.

 

[PeterDonis]

there is, unfortunately, a textbook that uses this

Later, he introduces a "proper 4-velocity"

Hm. So instead of using the standard meaning for "4-velocity" that every other source uses, he invents his own and then calls the standard 4-velocity "proper 4-velocity".

I would expect people who try to learn SR from this textbook to become very confused when they encounter the rest of the literature. Not to mention when they try to learn GR.

It's especially disappointing that this book claims to be about "the geometry of spacetime" but then focuses on things that aren't geometric invariants. It would be like trying to teach vector analysis in ordinary Euclidean 3-space by inventing a "vector length" that changed when you rotated your coordinates.

 

[vanhees71]

I think you mean null trajectories in spacetime?

of course, it must read "null trajectories in spacetime".

 

[vanhees71]

In many particle physics calculations, we model a photon with a 4-momentum (which is of course null).
With that photon 4-momentum, we use conservation of total 4-momenta
to work out the Compton Effect, neutral pion decay, etc...

Yes, and that's of course the correct description of a photon as an asymptotic free single-quantum Fock state. As already mentioned above, the description in terms of a null trajectory of a massless particle in GR is in fact to be interpreted as a solution of the Maxwell equation in the eikonal approximation. The null worldline of course does not admit the definition of a proper time and does also not the definition of a four velocity.

The lightlike tangent four-vector is instead "normalized" such that it defines the frequency of the photon at emission as it's time-like component for an observer in a local inertial frame with four-velocity $u^{\mu}$, i.e. $g_{\mu \nu}u^{\mu} \dot{x}^{\nu}(\lambda_0)=\omega_0$. Then the propagation of the wave to another spacetime point is described in terms of the lightlike four-vector along the null-world line (if there's no scattering due to mater, it's a null geodesics) to this point using the so determined affine parameter of the null worldline.