Verifying Kirchoff's law in an AC RLC circuit

[Felipe Lincoln]

Homework Statement

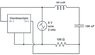
I have the following RLC circuit with an sinusoidal voltage generator and I want to verify the Kirchoff's first law with an oscilloscope. To measure the peak voltage in each of the components I just permute the positions between the component and the resistor.

The question is: If I sum all the peak tension, will I get $\mathcal{E} = V_R + V_C + V_L$ ?
Next question: if I measure each component's voltage with and voltmeter in AC mode, will the result be the same as before?

Homework Equations

The Attempt at a Solution

 

[BvU]

Hello Felipe,

You'll have to show an attempt at solution -- see guidelines

And list some relevant equations. This way potential helpers cannot distinguish if and how much you know about phase, complex impedance, etcetera.

In the mean time: answers are "No" and "I don't know what you mean with: as before"

Do you do all this on paper or do you have a screen shot of the oscilloscope picture ?
If so, what have you observed ?

Furthermore: 2kHz is a very low frequency compared to the resonance frequency of this circuit, so AC effects are rather small.

 

[Felipe Lincoln]

I'm almost sure that the answer for my both questions are NO. since the peak voltage does not occur in the same time in the oscilloscope and the AC voltmeter just take the $1/\sqrt{2}$ of the peak voltage it would result the same. Am I right ?

 

[Felipe Lincoln]

Hi friend, sorry about the incomplete thread.

Furthermore: 2kHz is a very low frequency compared to the resonance frequency of this circuit, so AC effects are rather small.

Isn't the resonance frequency $1/\sqrt{LC} = 2.4~\mathrm{kHz}$ ?

 

[BvU]

How did you calculate that ?

 

[BvU]

Never mind, I goofed 2.4 kHz it is.

 

[BvU]

So you have the reactance of the coil, of the capacitor and of the resistor. The voltage (on ch2 of the scope) over the latter gives you the current, so with the 5 V you get the reactance of the RLC series circuit.

You can sum all the peak voltages with $\mathcal{E} = V_R + V_C + V_L$, but that $\mathcal{E}$ has no physical meaning.

The AC meters usually give you $V_{\rm eff}$ as you indicate, so summing those AC measurements should give you $\mathcal{E}/\sqrt 2$

In short: I think you understand .

 

[Felipe Lincoln]

Yeah, after thinking a bit it already seems quite clear to me. Thank you friend