Verifying Stokes' Theorem help

In summary: The line integral on the left side is ∫c F • t ds. What does this represent?The line integral represents the distance that the function F is traveling over the interval [0,d]. What does this tell you about the function F?The function F is traveling a distance d over the interval [0,d]. This tells you that the function F is a continuous function.
  • #1
joe kutil
3
0

Homework Statement


Verify Stokes' theorem
∫c F • t ds = ∫∫s n ∇ × F dS
in each of the following cases:

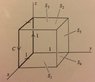
(a) F=i z2 + j y2
C, the square of side 1 lying in the x,z-plane and directed as shown
S, the five squares S1, S2, S3, S4, S5 as shown in the figure.

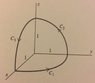
(b) F = iy + jz + kx
C, the three quarter circle arcs C1, C2, and C3 directed as shown in the figure.
S, the octant of the sphere x2 + y2 + z2 = 1 enclosed by the three arcs.

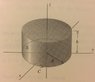
(c) F = iy - jx + kz
C, the circle of radius R lying in the xy-plae, centered at (0,0,0) and directed as shown in the figure.
S, the curved upper surfaces of the cylinder of radius R and height h.

Homework Equations


∫c F • t ds = ∫∫s n ∇ × F dS Stokes' theorem

The Attempt at a Solution


I have been staring at this problem for two weeks and every time I think i get it, i find out I'm wrong. Please help!
 

Attachments

  • FullSizeRender-1.jpg
    FullSizeRender-1.jpg
    36 KB · Views: 350
  • FullSizeRender-2.jpg
    FullSizeRender-2.jpg
    32.2 KB · Views: 354
  • FullSizeRender.jpg
    FullSizeRender.jpg
    46.7 KB · Views: 353
Physics news on Phys.org
  • #2
You need to calculate both sides of the equation and verify that you get the same thing.
Do you understand line integrals?
Do you know how to take the curl of a vector?
More importantly, the left and right sides of the equation tell you to execute a series of operations. Can you figure out what these are?
Start with the line integral on the left side. What do the symbols stand for?
 
  • #3
i understand how to take the curl, i just don't understand the concept of taking one over the surfaces
 
  • #4
joe kutil said:
i understand how to take the curl, i just don't understand the concept of taking one over the surfaces
Do you understand the meaning of all the symbols in ∫∫s n ∇ × F dS in terms of a picture?
Specifically
1. What does n represent?
2. What does S represent?
3. What is the relation between n and S?
Also note that the correct expression for the integrand is ##\hat{n} \cdot \vec{\nabla}\times \vec{F}dS.## The "dot" between n and ∇ × F is important and means more than "times".

If you don't know the answers to the three questions, please find out.
 
  • #5
Thank you I figured it out
 
  • #6
joe kutil said:
Thank you I figured it out
Great! Are you good to go with the line integral too?
 

What is Stokes' Theorem and why is it important?

Stokes' Theorem is a mathematical principle that relates the surface integral of a vector field over a surface to the line integral of the same vector field around the boundary of that surface. It is important because it allows us to calculate the circulation of a vector field over a closed surface, which has many real-world applications in fluid dynamics, electromagnetism, and other fields.

How do you verify Stokes' Theorem?

To verify Stokes' Theorem, you must first calculate the surface integral of the vector field over the given surface. Then, you must calculate the line integral of the same vector field around the boundary of that surface. If these two values are equal, then Stokes' Theorem is verified.

What are the prerequisites for understanding and verifying Stokes' Theorem?

A strong understanding of vector calculus, including line integrals, surface integrals, and vector fields, is necessary to understand and verify Stokes' Theorem. Additionally, knowledge of basic calculus and multivariable calculus is important.

What are some common mistakes when verifying Stokes' Theorem?

Some common mistakes when verifying Stokes' Theorem include miscalculating the surface integral or line integral, using the wrong orientation of the surface or boundary, and forgetting to account for the direction of the normal vector when calculating the surface integral.

Can Stokes' Theorem be applied to any vector field and surface?

Yes, Stokes' Theorem can be applied to any vector field and surface, as long as the surface is closed and the vector field is continuous and differentiable on the surface. However, in some cases, the calculations may be very difficult or impossible to perform by hand, so numerical or computational methods may be necessary.

Similar threads

Unable to simplify dS (Stokes' theorem)
    • Calculus and Beyond Homework Help
Replies
1
Views
606
Evaluating ∫cF⋅dr Using Stokes' Theorem
    • Calculus and Beyond Homework Help
Replies
2
Views
1K
Stokes' Theorem Example Question
    • Calculus and Beyond Homework Help
Replies
6
Views
1K
Applying Stokes' Theorem to the part of a Sphere Above a Plane
    • Calculus and Beyond Homework Help
Replies
21
Views
3K
Understanding Stokes' Theorem for a Specific Vector Field and Parametric Curve
    • Calculus and Beyond Homework Help
Replies
3
Views
1K
Determining between direct evaluation or vector theorems
    • Calculus and Beyond Homework Help
Replies
6
Views
2K
Another Stokes' Theorem Problem
    • Calculus and Beyond Homework Help
Replies
3
Views
1K
Applying Stokes' Theorem to Evaluate a Line Integral with a Parameterized Curve
    • Calculus and Beyond Homework Help
Replies
7
Views
2K
Verifying Stokes' theorem (orientation?)
    • Calculus and Beyond Homework Help
Replies
1
Views
3K
Find the Surface integral of a Paraboloid using Stoke's Theorem
    • Calculus and Beyond Homework Help
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top