Eitan Levy
- 259
- 11
- Homework Statement
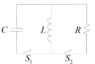
- In the circuit below the initial charge of the capacitor is Q. First, we shut S1 (S2 remains open) and wait for the first time in which the energy of the capacitor is minimal.
Then, we shut S2 and open S1 simultaneously. What is the voltage on the inductor right after the change?
- Relevant Equations
- ω=1/sqrt(LC)
I(t)=-ωQsin(ωt)
When the energy of the capacitor is minimal it has no charge therefore the voltage on it is 0. That means that the voltage on the inductor is 0 as well at the moment.
The part that confuses me is: why isn't the correct answer 0? How can a voltage change in a single moment?
Furthermore I am confused because in the solution, they used the fact that the current in the inductor before the change was Q/sqrt(LC) and therefore got the answer QR/sqrt(LC) . Why can the voltage shift like that but the current can not? How can we know what will remain constant (for a moment, in this case the current), and what may change instantly?
The part that confuses me is: why isn't the correct answer 0? How can a voltage change in a single moment?
Furthermore I am confused because in the solution, they used the fact that the current in the inductor before the change was Q/sqrt(LC) and therefore got the answer QR/sqrt(LC) . Why can the voltage shift like that but the current can not? How can we know what will remain constant (for a moment, in this case the current), and what may change instantly?