What is the maximum value of the current through the inductor?

[randomgamernerd]

1. Homework Statement : Two identical uncharged capacitors A and B each of capacitance C and an inductor L are arranged as shown in the adjacent figure. At t=0, the switch S1 is closed while switch S2 remains open.At time t=t_o=√(LC)Π/2, switch S2 is closed and S1 is opened.
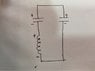
After switch S2 is closed and S1 is opened, find the maximum value of current through the inductor.

Homework Equations

: [/B]Kirchoff’s loop rule,
Q=CV for capacitor,
E=-LdI/dt for an inductor
I=I_osin(wt)
I_o=QW

The Attempt at a Solution

:[/B]
The question also asked to find out charge on capacitor at time t and also current through inductor at that instant. I have successfully found out the charge to be CE and current through inductor to be CE × 1/(√LC).
Now regarding the maximum current through inductor after time t=t_o, i am having problem.
I used Kirchoffs loop rule..
I assumed that charge on capacitor B is x, and that on A is CE-x.
then we have
LdI/dt= (CE-x)/C + x/C.
But then, x/C gets cancelled..
I think I am doing some mistake in assigning charges to the capacitor plates. Please help.

 

[haruspex]

LdI/dt= (CE-x)/C + x/C.

Think again about the signs.

 

[randomgamernerd]

Think again about the signs.

Yeah, I know i am doing something wrong there. Is this sign assigning(new attempt) correct?

.

 

[haruspex]

Yeah, I know i am doing something wrong there. Is this sign assigning(new attempt) correct? View attachment 225318.

Yes, but you need to assign quantities as in your earlier post and add the potentials up correctly.

 

[randomgamernerd]

Yes, but you need to assign quantities as in your earlier post and add the potentials up correctly.

ok, i am trying this sum again now..
okay, so now I have:
LdI/dt = (2x-CE)/C
Differentiating with respect to time,
Ld²I/dt²=2I/C
This gives me a new equation, and now w’=√(2/LC)
Initially current was CE/√LC.

Since there is already some current initially, I think the equation should be I=I₂sin(w’t +φ)
I₂=Qw’.
what is this new Q? how do I find this?

 

[randomgamernerd]

Yes, but you need to assign quantities as in your earlier post and add the potentials up correctly.

Please check post #5

 

[haruspex]

Since there is already some current initially,

Is there? I thought t₀ had been chosen so that there is not.

what is this new Q? how do I find this?

It's SHM. Total energy will be constant.

Edit: my mistake, at t₀ the current will be at a peak for the initial circuit.

 

[randomgamernerd]

Is there? I thought t₀ had been chosen so that there is not.

At t₀ , there is current through inductor before opening s1 and closing S2. That current will still remain when the change is made, am i right? or am i going wrong somewhere?[emoji28]

It's SHM. Total energy will be constant.

Oh yes! I will try once again.

 

[haruspex]

At t₀ , there is current through inductor before opening s1 and closing S2. That current will still remain when the change is made, am i right? or am i going wrong somewhere?[emoji28]

In the first part, with S₁ closed, what is the equation for current as a function of time?

 

[randomgamernerd]

In the first part, with S₁ closed, what is the equation for current as a function of time?

I got I=I₀Sinwt
where I₀=Q₀w,
Q₀ being CE

 

[randomgamernerd]

It's SHM. Total energy will be constant.

So here goes my attempt:
total energy remains constant.
Hence,
1/2Li² + q²/2C = constant...(A)
At time t=t₀,
I=CE/√LC , q=CE. Now here comes another confusion. Regarding the C I am denominator of equation A, should i take value of capacitance as just C or should it be the equivalent capacitance? if its the later case, I assume they are in parallel. Right? because same side plates have same signs.

 

[haruspex]

assume they are in parallel.

Don't be confused by the leftmost part of the original circuit. With S₁ open you can remove that. You just have the inductor and two capacitors connected ... how?

 

[randomgamernerd]

Don't be confused by the leftmost part of the original circuit. With S₁ open you can remove that. You just have the inductor and two capacitors connected ... how?

But the way I have assigned the signs in post #3, won't I consider that they are in parallel?
(Although I am getting the correct amswer if I assume them to be I am series, but just confirming all the concepts)
Do these signs have no role in deciding if two capacitors are in series or parallel? (because the leftmost capacitor acts like a cell after t₀)
Having equal potential difference is the only condition?

 

[haruspex]

But the way I have assigned the signs in post #3, won't I consider that they are in parallel?

No.
If you ignore the inductor, just treating that as a conductor, it is not possible to say whether the capacitors are in series or in parallel. It depends what points you take as their connection to the outside world.
If you take those points as being on the top horizontal wire and the bottom horizontal wire then they are in parallel; if as the ends of the inductor then they are in series.
I agree it is unusual to see that charge pattern on capacitors in series, but it is just a consequence of how they have been charged.

 

[randomgamernerd]

No.
If you ignore the inductor, just treating that as a conductor, it is not possible to say whether the capacitors are in series or in parallel. It depends what points you take as their connection to the outside world.
If you take those points as being on the top horizontal wire and the bottom horizontal wire then they are in parallel; if as the ends of the inductor then they are in series.
I agree it is unusual to see that charge pattern on capacitors in series, but it is just a consequence of how they have been charged.

okay, and what about a case like this?

Here is this not equivalent to a circuit where C₁ and C₃ are in series and C₂ is conncected in parallel to them?

 

[haruspex]

okay, and what about a case like this?View attachment 225366

Here is this not equivalent to a circuit where C₁ and C₃ are in series and C₂ is conncected in parallel to them?

Yes, but as I wrote, it depends where you take the connections to the outside to be. It could turn out to be three capacitors in series, or any two in series with the third in parallel to that pair.

 

[randomgamernerd]

Yes, but as I wrote, it depends where you take the connections to the outside to be. It could turn out to be three capacitors in series, or any two in series with the third in parallel to that pair.

In image posted in #15, this is only what has been given in the question and we were asked to calculate final charge on each capacitor

So do I consider them in series or not while calculating common potential?
I am confused[emoji28]

 

[haruspex]

do I consider them in series or not while calculating common potential?

There will be three potentials. You can assign unknowns to those, and to the charges, and write out an equation for each capacitor.
Or you could treat two as in series and just write equations for those as a single capacitor and for the other by itself.

 

[randomgamernerd]

There will be three potentials. You can assign unknowns to those, and to the charges, and write out an equation for each capacitor.
Or you could treat two as in series and just write equations for those as a single capacitor and for the other by itself.

[emoji848]Well, if i consider final charges on them be Q₁, Q₂, Q₃, then I am getting two equations, 1 from conservation of charge, and other from kirchhoffs loop rule. where do I get the third equation from?

 

[gneill]

At time t=to=√(LC)Π/2, switch S2 is closed and S1 is opened.

I find the above statement to be a bit problematical. Simultaneous switch changes where there is absolutely no time difference are pretty difficult (impossible) to manage in reality, and in this circuit the order of the switchings matters very much. This is due to there being no resistance to "slow" the charging of the "new" capacitor, hence it would charge to E instantaneously if S2 closes before S1 opens. However, if S1 opens before S2 closes, then the capacitor will receive no initial charge, and no new energy will be added to the oscillations. Even if the switchings are presumed simultaneous and instantaneous, what does it mean for the charging of the new capacitor which is also an instantaneous thing?

 

[haruspex]

1 from conservation of charge,

Two? These are not conductors.

 

[randomgamernerd]

Two? These are not conductors.

Did not get the point

 

[haruspex]

Did not get the point

There are three parts to the circuit, with charge being conserved within each.

 

[randomgamernerd]

There are three parts to the circuit, with charge being conserved within each.

Still confused. what do you mean by charge being conserved within each part [emoji29] ? Am I missing some point? or may be I'm not aware of the concept you are referring to[emoji27]

 

[haruspex]

Still confused. what do you mean by charge being conserved within each part [emoji29] ? Am I missing some point? or may be I'm not aware of the concept you are referring to[emoji27]

In your diagram for the initial state, the wire across the bottom connects the negative side of C₂ with the negative side of C₃. Those two negative plates have some total charge between them. Charge cannot pass through a capacitor, so that total will not change.

 

[randomgamernerd]

In your diagram for the initial state, the wire across the bottom connects the negative side of C₂ with the negative side of C₃. Those two negative plates have some total charge between them. Charge cannot pass through a capacitor, so that total will not change.

Oh yes! i had totally forgotten that concept..Thank you so much..Now I will try the sum again and if I get stuck again, i will post my work here so that you can point out my mistake [emoji28]

 

[randomgamernerd]

In your diagram for the initial state, the wire across the bottom connects the negative side of C₂ with the negative side of C₃. Those two negative plates have some total charge between them. Charge cannot pass through a capacitor, so that total will not change.

I’m so sorry for bothering again because of this one single sum, but could not reach the answer. I hope this os what you meant[emoji1427]

 

[haruspex]

I’m so sorry for bothering again because of this one single sum, but could not reach the answer. I hope this os what you meant[emoji1427]View attachment 225600

I'm confused. In the diagram above you have a box showing initial charges as 60, 90, 40. In the circuit itself, taking x as the change in charge, you use 20, 130, 0. In post #17 it was 40, 30, 10.
I can understand that you used x-40 as the change in charge. That would give the x you have at C₃ and the 20+x at C₁, but not the 130-x at C₂. So I think you made a sign error.

Edit: sorry, my sign error. Your working and answer are correct.

 

[randomgamernerd]

I'm confused. In the diagram above you have a box showing initial charges as 60, 90, 40. In the circuit itself, taking x as the change in charge, you use 20, 130, 0. In post #17 it was 40, 30, 10.

40, 30, 10 are the potential difference applied to charge the capacitros, not the charge itself.

I can understand that you used x-40 as the change in charge. That would give the x you have at C₃ and the 20+x at C₁, but not the 130-x at C₂. So I think you made a sign error.

Initially total charge is 60+90+40 = 190 ?
so charge on capacitor 2 is 190-(20+x +x-40)?
= 190-( 2x-20)
=210-2x
Am I correct now?

 

[haruspex]

40, 30, 10 are the potential difference applied to charge the capacitros, not the charge itself.

Initially total charge is 60+90+40 = 190 ?
so charge on capacitor 2 is 190-(20+x +x-40)?
= 190-( 2x-20)
=210-2x
Am I correct now?

Whoops... my mistake . Your answer in post #27 was correct.

 

[randomgamernerd]

Whoops... my mistake . Your answer in post #27 was correct.

But answer is not matching. They say its 380/13 for capacitor C3.[emoji27]

 

[haruspex]

40, 30, 10 are the potential difference applied to charge the capacitros, not the charge itself.

Good point.. but then, for C₁, 40*2=?

 

[randomgamernerd]

Good point.. but then, for C₁, 40*2=?

i am so sorry, it will be 80 and I have written 60. I am so sorry...I have got the answer now...I have this exam in a week and i don't know what will happen if i do mistakes like this. Thank you sir for your patience and helping me out. And also for reminding me of this concept. Thank you so much.

 

[haruspex]

i am so sorry, it will be 80 and I have written 60. I am so sorry...I have got the answer now...I have this exam in a week and i don't know what will happen if i do mistakes like this. Thank you sir for your patience and helping me out. And also for reminding me of this concept. Thank you so much.

There's no need to apologise to me. I made mistakes too on this one.

 

[randomgamernerd]

There's no need to apologise to me. I made mistakes too on this one.

[emoji28]