Voltage drop across a capacitor

[amolv06]

Homework Statement

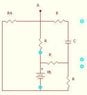
Below, I have attached a schematic that was on a test question for me. (NOTE: R4 = 4*r) We were supposed to find the current leaving the battery in terms of R, C, and Vb. The thing was, I had no idea what the voltage drop across the capacitor would be since there is no q given. How would one solve this?

Homework Equations

Kirchoff's laws
C=Q/V => V=Q/C
V=IR

The Attempt at a Solution

It's a bit hard showing since I would have a hard time drawing in all the loops and such, but I had 3 loops. I just didn't know what the equation for the one going through the top right would be since I'm not given q (or t).

I tried the following for the loop in question:

V_{b} - R(I_{2}+I_{3}) - IR_{3} - \frac{q}{c} - R(I_{3} + I_{1})=0

 

[berkeman]

Did the problem state that it was in steady-state? If so, the capacitor is an open circuit. If you were given some initial conditions different from the steady state condition, were you asked to calculate the response over time as the circuit moved to the final steady state solution? If so, then you need to solve the differential equation that you get when you put in the current-voltage relationship for a capacitor:

i(t) = C\frac {dv(t)}{dt}