Voltage gain of a bipolar transistor circuit

[eyeweyew]

TL;DR Summary

If base-to-collector voltage gain is negative, base-to-emitter voltage gain is positive, should emitter-to-collector voltage gain negative as a result of multiplying base-to-collector gain by the inverse of base-to-emitter gain? How come emitter-to-collector gain is positive?

For a simple bipolar transistor above, base-to-collector voltage gain ≈ -gm*Rc/(1+gm*Re) < 0, base-to-emitter voltage gain ≈ 1 > 0, should emitter-to-collector voltage gain ≈ -gm*Rc/(1+gm*Re) * 1 < 0. How come it is equal to gm*Rc > 0?

 

[eyeweyew]

I think I know why. Compute this way would only give indirect gain from emitter to collector.

 

[tech99]

Why are we multiplying the two gain figures? The output voltages are in series, so if being referenced to ground they are subtracted to obtain the signal voltage between the collector and emitter.

 

[DaveE]

Are you asking about the common base BJT amplifier?
https://www.electronics-tutorials.ws/amplifier/common-base-amplifier.html

 

[eyeweyew]

I guess a better way to rephrase my question is why base-to-collector voltage gain(common emitter) vc/vb does not equal to emitter-to-collector voltage gain(common base) vc/ve multiplied by base-to-emitter voltage gain(emitter follower) ve/vb?

I believe it is related to inspection analysis limitations for circuit with feedback.

 

[Averagesupernova]

The voltage gain of transistor circuits is determined by more than just the transistor. Resistors in the circuit have alot to do with the voltage gain.

 

[Tom.G]

I guess a better way to rephrase my question is why base-to-collector voltage gain vc/vb does not equal to emitter-to-collector voltage gain vc/ve multiplied by base-to-emitter voltage gain ve/vb?

Lets try this.

Recall that a transistor is a current amplifier, the Collector current is proportional to the base current.

Also realize that the Collector current has to flow thru the Emitter.

The result is that with similiar currents, the voltage gains at the Collector and at the Emitter are determined by the resistor values - similiar resistor values yields similiar voltage gains.

There is, however, a slight Fudge Factor.

The "Fudge Factor" needed comes when you realize that the Base current also flows thru the Emitter.

A detailed explanation can be found at:
https://www.electronics-tutorials.ws/amplifier/phase-splitter.html

(above link, and many more, found with:
https://www.google.com/search?hl=en&q=phase+splitter+circuit)

Cheers,
Tom

 

[LvW]

For a simple bipolar transistor above, base-to-collector voltage gain ≈ -gm*Rc/(1+gm*Re) < 0,

This gain formula for a common-emitter gain stage with negative Re-feedback is correct - however, only in case the signal source is connected DIRECTLY to the base node (via a coupling capacitor).
When there is a resistor Rb (as in your drawing) this resistor forms a voltage divider Rb-r_in and the gain will be correspondingly lower (r_in=dynamic signal input resistance at the base node).

Just for your understanding; "Negative gain" means nothing else than a phase inversion (180deg phase shift) between the signal voltage at the base node and the output voltage at the collector.

 

[DaveE]

Recall that a transistor is a current amplifier

Yes. I find these circuits much simpler to understand and solve if, at the device level, you think in terms of currents, not voltages. Of course voltages make currents and vice-versa.

Most of your questions can be clarified if you redraw your circuit using the basic T model of a BJT shown here.

Some like to move the small signal emitter resistor $r_e$ to the base, where its value becomes $(\beta + 1) r_e$. Although you'll often see $\beta r_e$, since $\beta + 1 \approx \beta$ for high gain devices.

 

[Baluncore]

To quickly identify the BJT polarity in the circuit, draw the symbolic arrow head on the emitter. Also, identify the polarity of Vs.

 

[LvW]

Most of your questions can be clarified if you redraw your circuit using the basic T model of a BJT shown here.

Some like to move the small signal emitter resistor $r_e$ to the base, where its value becomes $(\beta + 1) r_e$. Although you'll often see $\beta r_e$, since $\beta + 1 \approx \beta$ for high gain devices.

I like to mention that there are two other small-signal equivalent circuit diagrams for a bipolar transistor, which - according to my opinion - are much better and clearer than the mentioned T-model. These two models are much closer to the real transistor function (although the T-model works - if applied properly!).
Why?
* Because the T-model containes a quantity re which can be the cause for some misinterpretations and misunderstandings.
* At first, one must know that re is a dynamic quantity (not constant) which depends on the DC quiescent current .
* From the physical point of view it is not a resistance (although it has the unit V/A) and it does not belong to the emitter. Instead, it is an abbreviation (symbol) for the invers transconductance gm=1/re.
* Misinterpretations can occur when someone thinks that such a quantity (located in the emitter path) could have any influence on the DC operating point and/or could cause negative feedback.
* More than that - looking into the base node of the model (Fig. 3 in the linked doc) one could have the impression (visual inspection) that the input resistance would be identical to re (which is wrong).

 

[DaveE]

I like to mention that there are two other small-signal equivalent circuit diagrams for a bipolar transistor, which - according to my opinion - are much better and clearer than the mentioned T-model. These two models are much closer to the real transistor function (although the T-model works - if applied properly!).
Why?
* Because the T-model containes a quantity re which can be the cause for some misinterpretations and misunderstandings.
* At first, one must know that re is a dynamic quantity (not constant) which depends on the DC quiescent current .
* From the physical point of view it is not a resistance (although it has the unit V/A) and it does not belong to the emitter. Instead, it is an abbreviation (symbol) for the invers transconductance gm=1/re.
* Misinterpretations can occur when someone thinks that such a quantity (located in the emitter path) could have any influence on the DC operating point and/or could cause negative feedback.
* More than that - looking into the base node of the model (Fig. 3 in the linked doc) one could have the impression (visual inspection) that the input resistance would be identical to re (which is wrong).

Yes, that's how it is with simple models. They're wrong. That's what makes them simple.

 

[Averagesupernova]

Re' is what we called it in school. I assume this is what is referred to as re in the above posts. Normally it was set at 25 ohms for the math we did concerning the circuits we worked with. As said, it varies with emitter current. Re' is one of the things that determine input impedance at the base. Re' will also have a hand in determining signal gain especially when the emitter resistor is bypassed with a capacitor. Of course this is assuming common emitter configuration.
-
The numbers don't come out perfect, but they are close

 

[LvW]

Re' is what we called it in school. I assume this is what is referred to as re in the above posts. Normally it was set at 25 ohms for the math we did concerning the circuits we worked with. As said, it varies with emitter current. Re' is one of the things that determine input impedance at the base. Re' will also have a hand in determining signal gain especially when the emitter resistor is bypassed with a capacitor. Of course this is assuming common emitter configuration.
-
The numbers don't come out perfect, but they are close

With all respect - your post demonstrates how misinterpretations (and mistakes) can occur using the T-model. In your post, the small-signal quantity 1/gm (inverse transconductance) is written with capital letters as Re´. This looks like a classical ohmic resistor.
The problem is that, in particular, beginners are using such small-signal equivalent diagrams - and a misinterpretation of this model would be fatal.
Experienced people do not need such eqivalent diagrams - they know how a transistor works and do not need any model.

 

[Averagesupernova]

My bad. It's actually r'e. So you can blame me for confusing the 'inexperienced'. So, @LvW, are you 'experienced' or 'inexperienced' in that you didn't catch my mistake with Re' vs r'e? The correct one (r'e) is right out of a text book.
-
The 'experienced' folks don't need a lot of things. That doesn't change the fact that a particular property of a transistor, or anything for that matter, exists and needs to be defined. BTW, this is not the first time I've seen something besides r'e defining that particular property of a transistor.

 

[DaveE]

Experienced people do not need such eqivalent diagrams - they know how a transistor works and do not need any model.

I have had some experience in this field and, yes, I use the simplest T (or Hybrid-π) model nearly always for BJTs. I probably won't draw it that way on paper, but that is exactly what I am thinking about. Step 1 is figure out roughly what the circuit does (amplifier or oscillator, saturated or linear, high or low power, closed or open loop, etc.) More complex stuff is added later only as needed.

We all use models, real components are complicated things. I also only use about 5 digits in π.

 

[nazmulisrony]

The voltage gain of a bipolar transistor circuit primarily depends on the configuration used, such as common emitter, common base, or common collector. In a common emitter configuration, which is widely used, the voltage gain (A_v) can be approximated by the formula:


A_v = - \frac{\beta \times R_C}{r_e}


where:

• \beta is the current gain of the transistor.
• R_C is the load resistor in the collector.
• r_e is the internal emitter resistance, which is approximately \frac{26 mV}{I_E} at room temperature.

To get a deeper understanding of the working principle and the structure of bipolar junction transistors (BJTs), you can check out this detailed guide on [Link to personal website redacted by the Mentors]

 

[DaveE]

The voltage gain of a bipolar transistor circuit primarily depends on the configuration used, such as common emitter, common base, or common collector. In a common emitter configuration, which is widely used, the voltage gain (A_v) can be approximated by the formula:


A_v = - \frac{\beta \times R_C}{r_e}


where:

• \beta is the current gain of the transistor.
• R_C is the load resistor in the collector.
• r_e is the internal emitter resistance, which is approximately \frac{26 mV}{I_E} at room temperature.

To get a deeper understanding of the working principle and the structure of bipolar junction transistors (BJTs), you can check out this detailed guide on [Link to personal website redacted by the Mentors]

1) FYI, this thread is 8 months old. Which is OK if you have something to add or questions.
2) Recheck your formula. In the simplest model β doesn't appear.
3) There is a LaTeX guide available by clicking the link below and to the right of the reply window, or by searching the site.

 

[LvW]

To get a deeper understanding of the working principle and the structure of bipolar junction transistors (BJTs), you can check out this detailed guide on [Link to personal website redacted by the Mentors]

I do NOT recommend the linked document because it contains errors.
Example:
(Quote):
Out of 100% of the Emitter’s electrons, less than 1% are responsible for creating the Base current, while over 99% create the Collector current."
........................
........................
BJTs amplify signals by controlling the current flow through the base-emitter junction, where a small input current in the base leads to a larger output current in the collector, thusamplifying the signal.
(End of Quote).

This sounds a bit contradictory, does it not?
This is, because the statement in the last quoted sentence is simply wrong.
BJT`s amplify signals by controlling the VOLTAGE across the base-emitter junction - and, as a consequence, it is the transconductance (slope of the Ic=f(Vbe) curve) gm=d(Ic)/d(Vbe) which determines the voltage gain.

The base current is nothing else than an unwanted by-product. (The great late Barrie Gilbert calls it "a defect, a nuisance")

More than that, you wrote "r_e is the internal emitter resistance".
This is not correct and can lead to severe misunderstandings.
The quantity "r_e" does not belong to the emitter and it is not a resistance at all.
It is nothing else than the inverse of the transconductance (r_e=1/gm)
Hence, the dimension of r_e is ohms=volts/ampere , nevertheless, it is not a resistance (which always is a two-pole).

 

[Tom.G]

BJTs amplify signals by controlling the current flow through the base-emitter junction, where a small input current in the base leads to a larger output current in the collector, thusamplifying the signal.
(End of Quote).

This sounds a bit contradictory, does it not?
This is, because the statement in the last quoted sentence is simply wrong.
BJT`s amplify signals by controlling the VOLTAGE across the base-emitter junction - and, as a consequence, it is the transconductance (slope of the Ic=f(Vbe) curve) gm=d(Ic)/d(Vbe) which determines the voltage gain.

You may have confused a Bipolar transistor with a FET transistor.

I happen to disagree that your statements apply to a BJT (Bipolar Junction Transistor); they would apply to a FET if the base-emitter terminals were Gate-Source.

Also, gm (or transconductance, [output current]/[input voltage] ) is used to describe the transfer characteristic of a FET, a BJT is characterized by current transfer ratio, H_FE for DC or h_fe for AC [output current]/[input current].

See post https://www.physicsforums.com/posts/6985148/ above and --:

data sheet for:
2N555 https://alltransistors.com/transistor.php?transistor=4970

MOSFET description:
https://toshiba.semicon-storage.com...wledge/e-learning/discrete/chap3/chap3-6.html

Cheers,
Tom

 

[LvW]

You may have confused a Bipolar transistor with a FET transistor.

I happen to disagree that your statements apply to a BJT (Bipolar Junction Transistor); they would apply to a FET if the base-emitter terminals were Gate-Source.

Also, gm (or transconductance, [output current]/[input voltage] ) is used to describe the transfer characteristic of a FET, a BJT is characterized by current transfer ratio, H_FE for DC or h_fe for AC [output current]/[input current].

See post https://www.physicsforums.com/posts/6985148/ above and --:

data sheet for:
2N555 https://alltransistors.com/transistor.php?transistor=4970

MOSFET description:
https://toshiba.semicon-storage.com...wledge/e-learning/discrete/chap3/chap3-6.html

Cheers,
Tom

Hi Tom - thank you for your reply.
However, I like to repeat that the BJT is (like the FET) a transconductance device.
So I have not "confused" a BJT with a FET.
I am aware that there are many (unqualified) contributions (internet articles and even in some books) which state - without any evidence (!) - that the BJT would be current-driven. But this results from a misinterpretation of the known relation Ib=Ic/B.
We must not mathematically manipulate this equation (Ic=B*Ib) and think - at the same time - that physically we have changed the physical role of cause and effect.
Very good descriptions of the BJTs working principles can be found - for example - in "Art of Elecronics" (Horowitz/Hill) and in many detailed internet contributions from US universities (Berkeley, Harvard, MIT...). Did you read Barrie Gilberts comment (as quoted in my former contribution) ?

Please note that there are many theoretical explanations, observations and measurements which clearly prove that the BJT is voltage-driven.
On the other side - there is not a single proof for the claim that Ic would be controlled by Ic.
More than that - all the known rules for designing a good working gain stage are based on and derived from Shockleys well known formula Ic=f(Vbe) which leads to the definition of the transconductance gm=Ic/Vt.
Do you need further details?

Question: Can you explain the working principle of (a) Re-feedback or (b) current mirrors or (c) cascode stages or (d) class-B amplifiers with a current-steering mechanism?
Regards
LvW

 

[Averagesupernova]

I have taken the side of the bjt being current controlled in the past. It really makes no difference to me. I see both sides. But concerning this:

Question: Can you explain the working principle of (a) Re-feedback or (b) current mirrors or (c) cascode stages or (d) class-B amplifiers with a current-steering mechanism?
Regards
LvW

I will comment on the Re-feedback. I have worked with direct couple amplifiers where the collector of the first stage is directly tied to the emitter of the second stage. So first stage is common emitter and second stage is common base. No voltage signal shows up at the emitter of the common base stage. In reality there is a very very small signal at the emitter. Since the base of this stage is at AC ground, we can't expect much of a signal on the emitter if this is to remain a linear amplifier. So in actuality, the signal voltage across the base-emitter in this stage (common base) is the very same tiny signal voltage across the base-emitter in the common emitter in the previous stage. So I can't say I disagree with you @LvW but I will tell you that the Re feedback you mention isn't really relevant to your argument. There is ALWAYS feedback with a resistor in series with a diode. A resistor in series with the base of a transistor with a grounded emitter technically is providing feedback. It may be a poor design choice due to other reasons.

 

[LvW]

I have taken the side of the bjt being current controlled in the past. It really makes no difference to me. I see both sides. But concerning this:

..... I will tell you that the Re feedback you mention isn't really relevant to your argument. There is ALWAYS feedback with a resistor in series with a diode. A resistor in series with the base of a transistor with a grounded emitter technically is providing feedback. It may be a poor design choice due to other reasons.

Thank you for your contribution to the discussion.
Let me explain my arguments concerning Re-Feedback.
* Any unwanted increase in Ic - for example, caused by temperature increase - will increase the voltage drop across Re and, hence, the emitter voltage Ve. As a consequence, the base-emitter voltage Vbe=Vb-Ve will be reduced causing a corresponding Ic decrease.
* In summary: The resistor Re provides negative feedback.
* Now the question: Can this effect be regarded as a proof for voltage control (because the current Ib will also be decreased along with Ie) ? With other words: Will Re provide voltage or current feedback?
* My answer is "YES" - it is the voltage Ve across Re which provides the feedback effect (and the decrease in Ic) because the input impedance of the whole stage is increased due to Re.
Remember: From system theory we know that only voltage feedback causes an input impedance increase. Current feedback will always reduce the input impedance.

 

[Bullington]

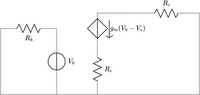
I think the original poster's questions have not been answered; these are the questions I will answer and I hope I have interpreted correctly:

1) How can I verify the bjt voltage gain from

1) base to emitter

2) base to collector

3) emitter to collector

2) If I have $\frac{V_c}{V_b}$ and $\frac{V_e}{V_b}$ how come $\frac{V_c}{V_b}\times \frac{V_b}{V_e} \neq \frac{V_c}{V_e}$



In the original figure there are many voltage sources with only labels so below I have attached the same figure with voltage sources added.

At this point it's nice to notice two things:

1) there are 2 total voltage sources and none are at the base, emitter or collector. So, finding the "voltage gain from $a$ to $b$" will mean that I must turn off all sources that I am not interested in and add a voltage source at $a$ and solve for the voltage at $b$.

2) I am looking for the linearized transfer, so while there are many ways to model a BJT; the simplest for our case is to say: $I_{ce}=g_m(V_b-V_e)$

So, lets answer the questions:

1. Solving the voltage gain from the base to emitter with all sources off I add a voltage source at $V_b$ which becomes:

$V_e=R_eg_m(V_b-V_e)$

Solving for $V_e$ I get:

$\left.\frac{V_e}{V_b}\right|_{V_{in}=0,V_{s}=0}=\frac{R_eg_m}{1+R_eg_m}$

Here I directly state $V_{in}$ and $V_s$ must be off.

This result can be further simplified by claiming $R_eg_m\ggg 1$ then I have your result $\left.\frac{V_e}{V_b}\right|_{V_{in}=0,V_s=0} \approx 1$

2. Solving the voltage gain from the base to collecter becomes:

$V_c=I_cR_c=(-g_m(V_b-V_e))R_c$

I know $V_e$ in terms of $V_b$ from above so:

$V_c=(-g_m(V_b-V_e))R_c=(-g_m(1-\frac{R_eg_m}{1+R_eg_m}))R_cV_b$

$\left.\frac{V_c}{V_b}\right|_{V_{in}=0,V_s=0}=\frac{-g_mR_c}{1+R_eg_m}$

3. Solving the Voltage gain from the emitter to the collecter I have to place a voltage source at the emitter and get the following:

$V_c=R_cI_c=R_c(-g_m(V_b-V_e))$

Notice that the dependent current source depends on V_b so it must be a known quantity, I set it to zero $V_b=0$ so I get:

$\left.\frac{V_c}{V_e}\right|_{V_{in}=0,V_s=0,V_b=0}=R_cg_m$

Finally, the last question: to find the emitter to collector gain I have to have a known base voltage; the base to emitter and base to collector transfers assume the base voltage can be anything, where the emitter to collector assumes that it must be constant, so strictly speaking they are not the same, ie:
$\left.\frac{V_c}{V_e}\right|_{V_{in}=0,V_s=0} \neq \left.\frac{V_c}{V_e}\right|_{V_{in}=0,V_s=0,V_b=0}$