P1nkButt3rflys
- 16
- 0
A) The graph shows V-I curves for two conductors. One is measured for a carbon resistor and obeys Ohm's law; the other is for a light-emitting diode (LED) and shows non-ohmic behaviour. What is the resistance of the carbon resistor?
B) For what value of current is the resistance of the LED the same as that of the carbon resistor? (Use a ruler and a triangle to draw on the diagram.)
I got the first portion. The carbon resistor is the linear line and the LED is the curved line. Using the graph I found R = 10 ohm for A. But cannot figure out how to solve B, any suggestions?
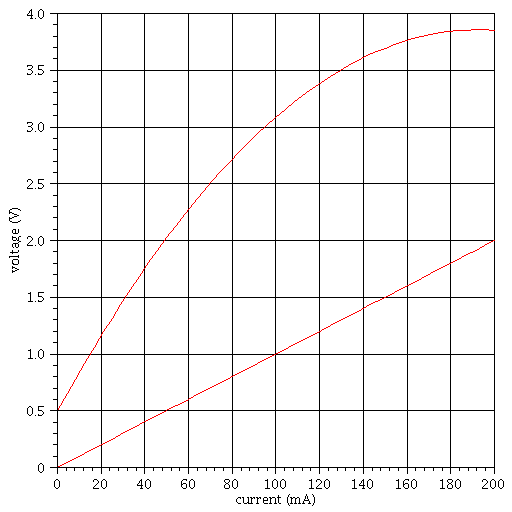
B) For what value of current is the resistance of the LED the same as that of the carbon resistor? (Use a ruler and a triangle to draw on the diagram.)
I got the first portion. The carbon resistor is the linear line and the LED is the curved line. Using the graph I found R = 10 ohm for A. But cannot figure out how to solve B, any suggestions?