SUMMARY
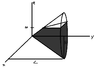
The discussion focuses on calculating the volume of a cone defined by the equation x² - y² - z² = 0, using multiple integrals. The correct approach involves using the formula for volume, Vol = ∭_R 1 dV, where R is the region of integration. The integrand should be 1, and the volume can be calculated by slicing the cone into laminae, preferably parallel to the xz-plane. The initial attempts at integration resulted in negative values, indicating a misunderstanding of the bounds or the integrand.
PREREQUISITES
- Understanding of triple integrals in calculus
- Familiarity with the geometric interpretation of volume
- Knowledge of the equation of a cone in three-dimensional space
- Ability to set appropriate limits for integration
NEXT STEPS
- Study the method of slicing volumes in calculus, focusing on laminae
- Learn about setting up triple integrals with correct bounds
- Explore the geometric properties of cones and their equations
- Practice integrating functions over specified regions using multiple integrals
USEFUL FOR
Students in calculus, particularly those studying multivariable calculus, as well as educators looking for examples of volume calculation using multiple integrals.