Volume of an oblique circular cone

[archaic]

Homework Statement

Find the volume of a circular cone.

Relevant Equations

N/A

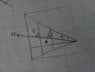
This is not homework. I have given myself two parameters; $\theta$, and $\alpha$. (see figure, it is a side view):
The idea is to find an expression for the radius of the circles as $x$ varies on that line (figure), then sum up infinitely many cylinders of infinitesimal thickness.
The radii all have an angle $\theta$ with the $x$-axis, and meet with the line making an angle $\alpha$ with the same axis at $x=b$, thus:
$$r(x)=\sqrt{(b-x)^2+(b\tan\alpha)^2}$$
To find $b$, I need to solve $(\tan\alpha)x-\tan\theta(x-b)=0$, which gives me:
$$b=\frac{\tan\theta-\tan\alpha}{\tan\theta}x$$
If the line upon which I put my $x$-axis has a length $a$, then the volume of the cone is:
$$\pi\int_0^ar^2(x)dx$$
Is the reasoning correct?
EDIT:
I could've also remembered triangles' similarities and notice that $\frac{R}{a}=\frac{r(x)}{x}$.

 

[hutchphd]

What is "a"? (I mean how do you define it.) The technique is correct until you encounter the "slanty" bottom of the cone. But notice you can cut the cone into a right angle cone and a slanty bottom piece. The slanty bottom part will have half the volume of a full cone bottom segment. So split the integral up.

 

[archaic]

What is "a"? (I mean how do you define it.) The technique is correct until you encounter the "slanty" bottom of the cone. But notice you can cut the cone into a right angle cone and a slanty bottom piece. The slanty bottom part will have half the volume of a full cone bottom segment. So split the integral up.

$a$ is the length which coincides with the $x$-axis.

 

[hutchphd]

You need a mathematical definition a=?
Also does the statement of the problem specify an oblique cone?

 

[archaic]

You need a mathematical definition a=?
Also does the statement of the problem specify an oblique cone?

$a$ is a constant. It is an exercise for myself, no statement, but no, general case.

 

[hutchphd]

Is ("a") shown on your picture...I don't know what it has to do with your question.

 

[archaic]

Is ("a") shown on your picture...I don't know what it has to do with your question.

 

[hutchphd]

Do you wish this to be an exercise in solid geometry or calculus? If calculus then you need to do the integral in 3 dimensions. If solid geometry you just need the solution regular cone and some intuition.
The drawing is not quite accurate if x is supposed to be the rotational axis of the cone...it will be lower at the left. And the simple interal you show will not be quite correct.

 

[archaic]

Do you wish this to be an exercise in solid geometry or calculus? If calculus then you need to do the integral in 3 dimensions. If solid geometry you just need the solution regular cone and some intuition.
The drawing is not quite accurate if x is supposed to be the rotational axis of the cone...it will be lower at the left. And the simple interal you show will not be quite correct.

Hello, I want to use calculus. I have had an answer from another person and, from how he tackled this problem, I see that the problem in my integral is that I considered the thickness to ne $dx$, but it should $dz=dx\sin\theta$.

 

[LCKurtz]

It's hard to tell from your graphic, but I'm not sure what you are describing is even a cone, slanted or not. Is the base curve a circle? Ellipse? Look at the following figure:

You should have a base and the cross sections should be similar as in the figure. The volume of any such solid is the one third the area of the base times the vertical height. I don't think the angle between a slant height and the center of the base to the vertex is constant. That's what I think you are calling $\alpha$.