Calculation of moment of inertia of cylindrical surface

[zenterix]

Homework Statement

(Apostol, Vol II, 2nd Ed., Chapter. 12.10, Problem 10)
A homogenous paper rectange of base $2\pi a$ and altitude $h$ is rolled to form a circular cylindrical surface $S$ of radius $a$. Calculate the moment of inertia of $S$ about an axis through a diameter of the circular base.

Relevant Equations

$I=\int\int_S r^2 dm$

Here is the homogenous paper rectangle

And if we roll it we get a cylinder with base radius $a$.

It is not clear to me what "an axis through a diameter of the circular base means".

Let's imagine such as axis is $\alpha$ in the following figure

Then we have

$$I_{\alpha}=\int_0^h\int_0^{2\pi} z^2 \cdot \frac{M}{4\pi a^2}ad\theta dz = \frac{Mh^3}{6a}\tag{1}$$

where I have used a mass density of $\frac{M}{4\pi a^2}$ for the cylindrical surface.

Now, technically, if we were to use the following axis instead

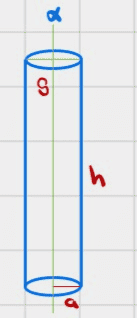
then it also "passes through" a diameter of the circular base. In this case we have

$$I_{\alpha}=\int_0^h\int_0^{2\pi} a^2\cdot \frac{M}{4\pi a^2} a d\theta dz=\frac{Mah}{2}$$

Neither one of these calculations matches the answer at the end of the book, which is $\pi a^3h+\frac{2}{3}\pi ah^3$.

What am I doing wrong here?

 

[BvU]

Hi,

Looking at your equation (1), it seems to me you have $r=z$, independent of $\theta$. That can't be right.

Looking at the book answer, it seems they assume $\rho = 1$.

For a hoop about a central diameter, here I find $I={1\over 2} Mr^2$.
(which also can be found with the perpendicular axis theorem -- see below)

With $r=a$ and $M = 2\pi a h\rho$ that reproduces the first term in the book solution.

(**)
The parallel axis theorem would add a second term for which I can't reproduce the book value .
(a naive $I = I_{cm} + Md^2$ with $d = {h\over 2}$ gets me ${1\over 2} \pi a h^3$)

I tink the answer lies here :

Hoop about diameter:$$dI_z = dI_x+dI_y\ \ \& \ \ dI_x=dI_y \Rightarrow dI_x = {1\over 2} dI_z = {1\over 2} dm R^2$$

Hoop about parallel axis at distance z:$$dI_x = {1\over 2} dm R^2 + dm\, z^2$$Integrate and now the second term also agrees with the book.

Bonus points for pointing out what's wrong with (**)
[edit] Earn my own bonus: hoop about diameter expression is for $h=0$

$\$

 

[Orodruin]

I believe the first option is what is asked for. What you are missing is that you should multiply the mass elements by the distance to the axis squared, this is not given by $z^2$. Can you figure out what it should be?

Hint: Your result is correct if $h \gg a$.

 

[Orodruin]

Hi,

Looking at your equation (1), it seems to me you have $r=z$, independent of $\theta$. That can't be right.

Looking at the book answer, it seems they assume $\rho = 1$.

For a hoop about a central diameter, here I find $I={1\over 2} Mr^2$.
(which also can be found with the perpendicular axis theorem -- see below)

With $r=a$ and $M = 2\pi a h\rho$ that reproduces the first term in the book solution.

(**)
The parallel axis theorem would add a second term for which I can't reproduce the book value .
(a naive $I = I_{cm} + Md^2$ with $d = {h\over 2}$ gets me ${1\over 2} \pi a h^3$)

I tink the answer lies here :

Hoop about diameter:$$dI_z = dI_x+dI_y\ \ \& \ \ dI_x=dI_y \Rightarrow dI_x = {1\over 2} dI_z = {1\over 2} dm R^2$$

Hoop about parallel axis at distance z:$$dI_x = {1\over 2} dm R^2 + dm\, z^2$$Integrate and now the second term also agrees with the book.

Bonus points for pointing out what's wrong with (**)
[edit] Earn my own bonus: hoop about diameter expression is for $h=0$

$\$

While you certainly can use the parallel axis theorem, I think the correct integral in itself is pretty straightforward.

 

[zenterix]

I believe the first option is what is asked for. What you are missing is that you should multiply the mass elements by the distance to the axis squared, this is not given by $z^2$. Can you figure out what it should be?

Hint: Your result is correct if $h \gg a$.

Oh, right, silly me.

$$I_{\alpha}=\int_0^h\int_0^{2\pi} (a^2\cos^2{\theta}+z^2)\cdot \frac{M}{4\pi a^2}\cdot a d\theta dz$$

$$=\frac{M}{4\pi a^2} \cdot (\pi a^3h +\frac{2}{3}\pi ah^3)$$

If we assume that the density is 1 then the result matches the book.