Water flows from a compressed tank

[Karol]

Homework Statement

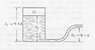
A tank of height 3.6[m] and closed at the top is filled with water to height 3[m], see drawing. the pressure P₁ above the water is 1.055[kgf/cm². A pipe is coming out from the bottom and the opening is 1.5[m] above the ground. what is the water's velocity out of the pipe when the water in the tank is at 3[m] and at 2.4[m]. neglect friction and assume the air expands isothermally.

Homework Equations

Bernoully equation: $\frac{v^2}{2}+gz+\frac{P}{ρ}=Const$
z=height, ρ=specific mass[kg/m³
Atmospheric pressure: 101,325[pa]
The specific mass of water=1000[kg/m³]
In an isothermic process: $P_1V_1=P_2V_2$

The Attempt at a Solution

The pressure above the water in pascals:
$$1.055\left[\frac{kgf}{cm^2}\right]=10.55\left[\frac{N}{cm^2}\right]=105,500\left[\frac{N}{m^2}=pa\right]$$
The left side is the outlet of the pipe. the zero for height is the pipe's exit:
$$\frac{v^2}{2}+\frac{101,325}{1000}=1.5\cdot 10+\frac{105,500}{1000}\rightarrow v=6.2\left[\frac{m}{sec}\right]$$
When the water lowers to 2.4[m] the pressure drops (A=base area of tank):
$$105,500\cdot A\cdot 0.6=P_2\cdot A\cdot 1.2\rightarrow P_2=52,570[pa]$$
$$\frac{v^2}{2}+\frac{101,325}{1000}=0.9\cdot 10+\frac{52,570}{1000}$$
It gives a negative sign, does it mean the water flows in?

 

[haruspex]

Since the pressure starts at only a little above 1 atm it will be down to about half an atm at 2.4m. A water height difference of only 0.9m is clearly not going to overcome half an atmosphere of push back. I don't see any errors in your working.
One small point... given the number of significant digits quoted for the pressures, you should probably use a more accurate number for g.

 

[Karol]

Very Thanks