ab200
- 13
- 3
- Homework Statement
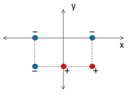
- Five charges are arranged as shown below. Each charge is either +1.5 nC (red) or -1.5 nC (blue). They are spaced by 1 cm intervals (each dotted line is 1 cm long). What is the potential, in V, at the origin?
How much work do you have to do, in electron volts (eV), to move an electron from infinitely far away to the origin?
- Relevant Equations
- V = kq/r
U = qV
Looking at the image, I see that due to symmetry, the bottom-left negative charge and the bottom-right positive charge cancel out, leaving me with a triangle around the center. I'm not entirely sure how to solve for potential at the origin specifically, but I believe that the potential energy of a system is equal to the external work needed to assemble it.
Thus, U = k [(q1q2 / r12) + (q2q3 / r23) + (q1q3 / r13)]. But I got a very, very small number that doesn't seem right, plus U is in joules, not volts. If I divide by 1.6e-19 to convert to volts, I get an enormous number that doesn't seem right either.
What am I doing wrong in terms of problems setup?
Thus, U = k [(q1q2 / r12) + (q2q3 / r23) + (q1q3 / r13)]. But I got a very, very small number that doesn't seem right, plus U is in joules, not volts. If I divide by 1.6e-19 to convert to volts, I get an enormous number that doesn't seem right either.
What am I doing wrong in terms of problems setup?