BeyondBelief96
- 14
- 2
Homework Statement
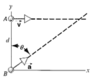
A particle A moves along the line y = d (30 m) with a constant velocity
Homework Equations
Kinematic Equations
The Attempt at a Solution
So I listed out all knowns and unknowns for both particle A & B as follows:
Particle A: Xi = 0, Xf = ?, Vix = 3 m/s, Vif = 3m/s, a = 0 t = ? and y = 30
Particle B: Xi = 0, Xf = ?, Vix = 0 m/s, Vif = ?, ax = asin(theta), t = ?
Yi = 0, Yf = 30, Viy = 0 m/s, Vif = ?, ay = acos(theta), t = ?
From there I used the kinematic equation d = vit + 1/2at^2 for particle A and B and got the following:
Particle A: x = 3t, y =30
Particle B: x = 1/2asin(theta)t^2, y = 1/2acos(theta)t^2
I set each of the equations equal to each other and tried to solve the system of equations for theta as follows:
3t = 1/2asin(theta)t^2 (Eq1)
30 = 1/2acos(theta)t^2 (Eq2)
3 = 1/2asin(theta)t so t = 6/asin(theta)
So I plugged t into Eq2:
30 = 1/2acos(theta)[6/asin(theta)]^2
from here I am at a loss on how to solve for theta. To be honest, my algebra solving skills arent super spectacular, which is a bit sad haha. I was able to simplify this as:
30 = 1/2acos(theta)[36/a^2sin^2(theta)] == 5/3 = cot(theta)/asin(theta) ...aaaaaand this is where I am lost.[/B]