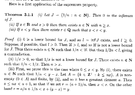MHB What Are the Key Insights from D. J. H. Garling's Theorem 3.1.1?

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume I: Foundations and Elementary Real Analysis ... ...

I am focused on Chapter 3: Convergent Sequences

I need some help to fully understand some remarks by Garling made after the proof of Theorem 3.1.1 ...Garling's statement and proof of Theorem 3.1.1 (together with the interesting remarks) reads as follows:

View attachment 9031
View attachment 9032
My questions on the remarks after the proof are as follows:
Question 1

In the remarks after the proof of Theorem 3.1.1 we read the following:

" ... ... There exists a least positive integer, $$q_0$$, say, such that 1$$/q_0 \lt y - x$$ ... ... "Can someone please explain exactly why this is true ... ..

Question 2

In the remarks after the proof of Theorem 3.1.1 we read the following:

" ... ... and there then exists a least integer, $$p_0$$, say, such that $$x \lt p_0 / q_0$$ ... ..."
Question 3

In the remarks after the proof of Theorem 3.1.1 we read the following:

" ... ... Then $$x \lt p_0 / q_0 \lt y$$ and $$r_0 = p_o / q_0$$ is uniquely determined ... ... "Can someone please explain exactly why this is true ... ..Help will be appreciated ...

Peter

 

[Olinguito]

In the remarks after the proof of Theorem 3.1.1 we read the following:

" ... ... There exists a least positive integer, $$q_0$$, say, such that 1$$/q_0 \lt y - x$$ ... ... "Can someone please explain exactly why this is true ... ..

Because $y-x>0$, so if you go $1,\frac12,\frac13,\ldots$ you will eventually come to an integer $n$ such that $y-x>\frac1n$. $q_0$ is the least such $n$.

Question 2

In the remarks after the proof of Theorem 3.1.1 we read the following:

" ... ... and there then exists a least integer, $$p_0$$, say, such that $$x \lt p_0 / q_0$$ ... ..."

Similar to above. We go $\frac1{q_0},\frac2{q_0},\frac3{q_0},\ldots$ until we come to an integer $m$ such that $x<\frac m{q_0}$; then $p_0$ is the least such integer $m$.

Question 3

In the remarks after the proof of Theorem 3.1.1 we read the following:

" ... ... Then $$x \lt p_0 / q_0 \lt y$$ and $$r_0 = p_o / q_0$$ is uniquely determined ... ... "Can someone please explain exactly why this is true ... ..

Because $q_0$ is the least integer $n$ such that $y-x>\frac1n$ and $p_0$ is the least integer $m$ such that $x<\frac m{q_0}$ – and those least integers are unique given $x$ and $y$. Note that this is not saying that there is a unique rational $r$ satisfying $x<r<y$ (which isn’t true since we know there are infinitely many rationals between $x$ and $y$); it is only saying that the process finds one particular rational between $x$ and $y$.

 

[Math Amateur]

Because $y-x>0$, so if you go $1,\frac12,\frac13,\ldots$ you will eventually come to an integer $n$ such that $y-x>\frac1n$. $q_0$ is the least such $n$.Similar to above. We go $\frac1{q_0},\frac2{q_0},\frac3{q_0},\ldots$ until we come to an integer $m$ such that $x<\frac m{q_0}$; then $p_0$ is the least such integer $m$.

Because $q_0$ is the least integer $n$ such that $y-x>\frac1n$ and $p_0$ is the least integer $m$ such that $x<\frac m{q_0}$ – and those least integers are unique given $x$ and $y$. Note that this is not saying that there is a unique rational $r$ satisfying $x<r<y$ (which isn’t true since we know there are infinitely many rationals between $x$ and $y$); it is only saying that the process finds one particular rational between $x$ and $y$.

Thanks Olinguito ... appreciate your reply and your help ...

But just a discussion point ...

You write:

" ... ... Because $y-x>0$, so if you go $1,\frac12,\frac13,\ldots$ you will eventually come to an integer $n$ such that $y-x>\frac1n$. $q_0$ is the least such $n$. ... ... "

Now what you have said is definitely very plausible ... but is it rigorous ... what do you think ... can you make a more rigorous argument ... ... does a more rigorous argument exist ... ?

Or am I overplaying and exaggerating (indeed perhaps misrepresenting ...? ) the idea of rigour ... particularly in a case where what is to be proved might be sensibly regarded as obvious ,,, what do you think ...

Indeed ... what is rigour anyway ...

Peter

 

[Olinguito]

You write:

" ... ... Because $y-x>0$, so if you go $1,\frac12,\frac13,\ldots$ you will eventually come to an integer $n$ such that $y-x>\frac1n$. $q_0$ is the least such $n$. ... ... "

Now what you have said is definitely very plausible ... but is it rigorous ... what do you think ... can you make a more rigorous argument ... ... does a more rigorous argument exist ... ?

Alternatively, you can take $q_0$ to be the smallest integer $n$ such that $n>\dfrac1{y-x}$.

 

[Math Amateur]

Alternatively, you can take $q_0$ to be the smallest integer $n$ such that $n>\dfrac1{y-x}$.

On reflection ... I have a further question ... concerning Garling's remark following the proof concerning statement (iii) ...

Garling's logic proceeds as follows:

We have $$x \gt 0$$ and we want to determine a rational $$r$$ with $$x \lt r \lt y$$.

We first determine the least positive integer $$q_0$$ such that $$1/q_0 \lt y - x$$ ...

We then determine the least positive integer such that such that $$x \lt p_0 / q_0$$

Then ...

... Garling claims we have $$x \lt p_0 / q_0 \lt y$$ ... ...

My question is as follows:

In the above process .. how are we sure that $$p_0 / q_0 \lt y$$ ... ... ?

Help will be appreciated ...

Peter

 

[Olinguito]

$p_0$ is the least integer such that $x<\dfrac{p_0}{q_0}$​

$\implies\ \dfrac{p_0-1}{q_0}\ \leqslant\ x$

$\implies\ \dfrac{p_0}{q_0}\ \leqslant\ x+\dfrac{p_0}{q_0}\ <\ x+y-x\ =\ y$.

 

[Math Amateur]

$p_0$ is the least integer such that $x<\dfrac{p_0}{q_0}$​

$\implies\ \dfrac{p_0-1}{q_0}\ \leqslant\ x$

$\implies\ \dfrac{p_0}{q_0}\ \leqslant\ x+\dfrac{p_0}{q_0}\ <\ x+y-x\ =\ y$.

Thanks for all your help, Olinguito ,,,

Peter