What are the practical limits of constructive interference?

[rumborak]

The "wireless power" thread made me think of this, but I have pondered it before when it comes to microphone arrays etc
You can easily find documentation on the interference patterns N in-line sources of waves generate. E.g.

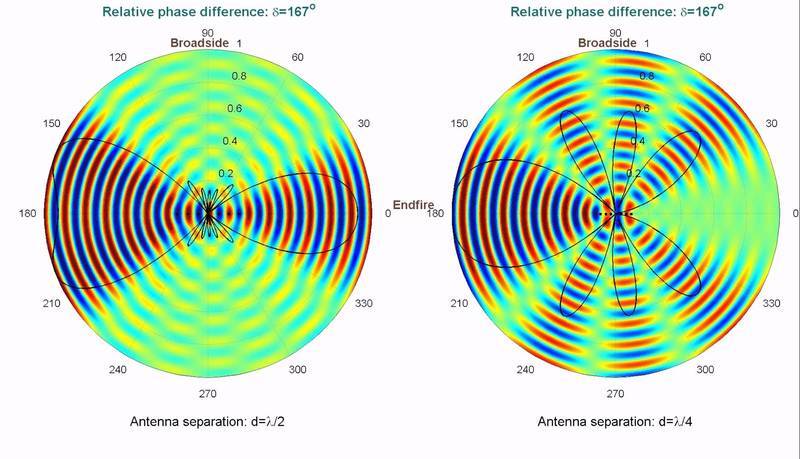
The annoying thing here is that you have infinitely extending lobes, which would be undesirable for something that tries to pinpoint delivery of (acoustic/EM) energy.
It would seem to me that for example a source arrangement in a triangle would allow some spatially constrained Maxima inside it; but are there simple rules of thumb for this type of thing that constrain the patterns? I can imagine that with a complete ring of sources you could probably reverse engineer any pattern with a Fourier analysis, but that's also overkill on the other end.

 

[anorlunda]

The military has several directed energy weapons.

If you search the references in this article, you may find things that pertain to your question.
https://en.wikipedia.org/wiki/Directed-energy_weapon
Especially this one
https://en.wikipedia.org/wiki/Directed-energy_weapon#Long_Range_Acoustic_Device_.28LRAD.29

 

[sophiecentaur]

The annoying thing here is that you have infinitely extending lobes, which would be undesirable for something that tries to pinpoint delivery of (acoustic/EM) energy.

This is a consequence of Diffraction. To direct energy in a specified direction with a certain required beam width you need an extended source. The narrower the required beam θ, the wider the necessary Aperture, d. (roughly θ = λ/2d) There are techniques for doing a bit better than the diffraction limit with 'Supergain Arrays' but there is not a lot of juice in that lemon. This is one of the reasons why Radiotelescopes are so enormous.