- #1
kmartin
- 10
- 0
Is it possible for a telescope to resolve images beyond the diffraction limit? In other words, is the information in the light entering a telescope insufficient to resolve beyond the diffraction limit, or is information lost when the light is focused onto a screen?
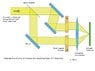
Attached to this post is a diagram of my thought experiment telescope design. The collimated output from a telescope is split into two beams. Each beam is then passed through a birefringent crystal, and then the two beams are focused down onto a single screen.
If, for example, the telescope is looking at two far away point sources (Point A and Point B), then the collimated beam will consist of two overlapping plane waves, traveling in slightly different directions. Because of the small difference in propagation direction, they will experience slightly different refractive indices when going through the birefringent crystals. This causes a difference in path lengths for light from point A compared to light from point B. If the path lengths are arranged so that light from point A constructively interferes at the focus point, and the correct length of birefringent crystals is chosen, then light from point B will interfere destructively. This allows light from point A to be separated from light from point B, even if this would be impossible conventionally due to the resolving power limit. By my calculations, if the collimated beam is 5mm in diameter, the birefringent crystals are made of calcite and 1.5cm long, and the light wavelength is around 500nm, then the resolving power of the telescope would be doubled. Using thicker crystals, or a more exotic crystal (e.g. calomel) could produce a much higher increase. Also the beam could be split multiple times to improve the resolving power in both dimensions, and to reduce the effects of interference patterns.
Note that the light experiences a 'walk off' as it enters and exits the crystal, as shown in the diagram, however this shouldn't affect the operation of the telescope. Also the phase difference from the change in refractive index is proportional to the angle between the propagation directions of the light from the two sources. This is much more significant than the geometric path difference, which is proportional to the square of the angle.
My telescope design can be thought of as similar to a system that combines the output from several telescopes into a single image. However in my design the alignment is much simpler, and there would be no spatial coherence issues, allowing for better nulling.
So would my telescope design work?
Attached to this post is a diagram of my thought experiment telescope design. The collimated output from a telescope is split into two beams. Each beam is then passed through a birefringent crystal, and then the two beams are focused down onto a single screen.
If, for example, the telescope is looking at two far away point sources (Point A and Point B), then the collimated beam will consist of two overlapping plane waves, traveling in slightly different directions. Because of the small difference in propagation direction, they will experience slightly different refractive indices when going through the birefringent crystals. This causes a difference in path lengths for light from point A compared to light from point B. If the path lengths are arranged so that light from point A constructively interferes at the focus point, and the correct length of birefringent crystals is chosen, then light from point B will interfere destructively. This allows light from point A to be separated from light from point B, even if this would be impossible conventionally due to the resolving power limit. By my calculations, if the collimated beam is 5mm in diameter, the birefringent crystals are made of calcite and 1.5cm long, and the light wavelength is around 500nm, then the resolving power of the telescope would be doubled. Using thicker crystals, or a more exotic crystal (e.g. calomel) could produce a much higher increase. Also the beam could be split multiple times to improve the resolving power in both dimensions, and to reduce the effects of interference patterns.
Note that the light experiences a 'walk off' as it enters and exits the crystal, as shown in the diagram, however this shouldn't affect the operation of the telescope. Also the phase difference from the change in refractive index is proportional to the angle between the propagation directions of the light from the two sources. This is much more significant than the geometric path difference, which is proportional to the square of the angle.
My telescope design can be thought of as similar to a system that combines the output from several telescopes into a single image. However in my design the alignment is much simpler, and there would be no spatial coherence issues, allowing for better nulling.
So would my telescope design work?