What does the Navier-Stokes equation look like after time discretization?

[Kukkat]

Hi,

I know the general form of the Navier Stokes Equation as follows.

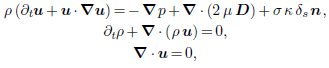
I am following a software paper of "Gerris flow solver written by Prof. S.Popinet"
[Link:http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.374.5979&rep=rep1&type=pdf]
and he mentions after time discretization he ends with the following equation:

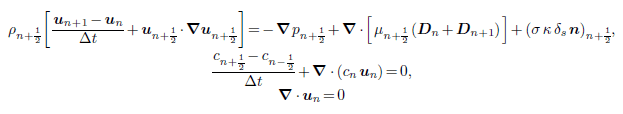
where n-1 is the previous time step, n+1 is the next time step and n+0.5 is mid time for the present time step.

Solving equation implicitly/ explicitly in time means solving for next time data however in the equation there are rather two unknowns u_n+0.5 and
u_n+1.

Not sure why he uses different terms at different time intervals. Density at n+0.5, velocity at n, n-1, n+0.5 etc..

Can anyone point me or explain me how he arrives at this specific sort of discretized equation.

 

[eys_physics]

The link to the paper doesn't work.

 

[Chestermiller]

I'm not familiar with this particular finite difference scheme, but presumably u_n+0.5 is already know when you are calculating u_n+1

 

[Kukkat]

Sorry for the link.
http://www.sciencedirect.com/science/article/pii/S002199910900240X

@Chestermiller guess that's true. It is being solved by the time step projection method which means an intermediate velocity is computed and later updated to a divergence free velocity by solving the laplace of pressure term as in the mentioned paper.

The notation is a bit strange for me as he uses density at time n+0.5 without solving any advection equation. From what I see density terms at n and n+0.5 should be the same.