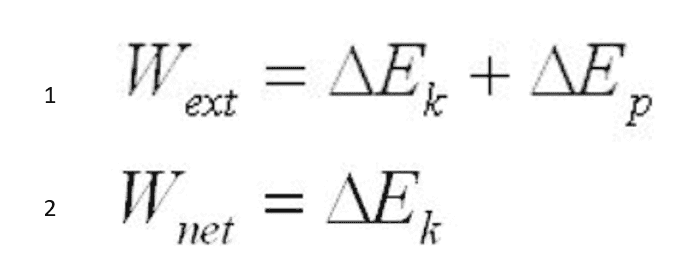Homework Help Overview
The discussion revolves around the Work-Energy theorem in physics, with participants exploring its definitions, equations, and implications. The original poster presents two equations related to the theorem and questions the correct terminology regarding external work. The conversation touches on the distinctions between conservative and non-conservative forces and their roles in the theorem.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants discuss the definitions of variables in the equations, the context of external versus internal forces, and the conditions under which the Work-Energy theorem applies. There are inquiries about the nature of forces involved and the interpretation of work done in specific scenarios.
Discussion Status
The discussion is active, with various interpretations and clarifications being offered. Some participants provide insights into the equations and their applications, while others express confusion and seek further clarification on the concepts. There is no explicit consensus, but several productive lines of inquiry are being explored.
Contextual Notes
Participants question the assumptions underlying the equations and the definitions of terms used. There is a focus on the relevance of conservative and non-conservative forces in the context of the Work-Energy theorem, as well as the implications of considering different systems.