What formula or principle governs this observed phenomena?

[VMey]

Hello,

Just discovered this forum as I'm so intensely curious about this question I sought out just such a place!

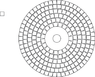
I'm currently designing a circular patio using 6-in square blocks in concentric circles. While using a combination of Excel and Adobe Illustrator, I uncovered something unexpected. Each new circle required a consistent number of additional blocks, when rounded up to the value of a whole block. 7 to be exact. It is my goal to understand how and why this works, and hopefully to learn a formula that will let me repeat it and change things like block size.

I began with a 36-inch circle which would be a firepit. I determined I would need 18.85 6-inch blocks. I'm not planning to cut them, so I rounded up to 19 blocks and backed into the circumference that would accommodate it (114 inches). I went to the next ring and more or less repeated the same process: approximated circumference, determined a fractional number of blocks, rounded up to nearest whole block, backed into precise circumference. Rinse, repeat.

After about six rings, I wanted to know how many rings I'd need to get to a 16-foot diameter, so I figured I'd average the diameter increase between each consecutive ring, hoping to extrapolate an estimate. I was surprised to find each circle was the exact same increase from its adjacent circle (1.114085 ft). And that's when I noticed the consistency in the blocks.

If I was aiming to have circumferences that accommodated only whole blocks, I learned that each new circle required exactly 7 additional blocks.

How is this so precise and predictable? I'm assuming it has something to do with effectively turning the circle into a polygon by using blocks, since they are flat. So the first "circle" is really a 19-sided polygon, the next a 26-sided polygon, etc. But I don't know the first thing about complex polygons.

Furthermore, I'd love learn HOW this works. If I had a formula of some kind, I could change the size of the blocks at will and speed up my estimates.

Thanks for any help! Attached an image for reference

 

[Simon Bridge]

I went a bit further ...

If you have blocks which are x wide and y long, and lay them in concentric circles with the long-axis radial, then each circle will have an inner diameter 2y longer than the last.

If we start, as you did, with the inner circumference rigged so a natural number, $b$, of blocks fits comfortably around it, then the inner circumference is $C_0=bx$; so the inner diameter is $D_0=bx/\pi$. The next circle out has an inner diameter of $D_1=bx/\pi +2y$ so the next circumference is $C_1=(bx/\pi +2y)\pi=bx+2\pi y$ ...

See the pattern?
The circumference for the nth circle will be $C_n=bx+2n\pi y$ and each circumference differs from the last by $\Delta C = 2\pi y$ which is a difference of $2\pi y/x$ blocks.

If y=x then that number will be $2\pi$ which is about 6.3 ... which gives an overlap of 2/3 of a block.
You could round down and have biggish gaps between bricks or round up to the next circumference, which is 7 blocks around.

Does that sound like what you did?

For square bricks this will leave a larger gap between circles that you may like - which can be fixed by making y slightly longer than x. You can reverse the above calculation to figure out what shape blocks to use for a circular pattern with a snug fit.

 

[Erland]

For every new circle of blocks you add, the radius of the circle which encloses all the blocks increases with 1 unit (= the side of the square block). But then, the circumference of the circle increases with 2π units, since the circumference is 2πr. This means that you can fit 2π≈6.28 more blocks in than the previous time. Rounding of upwards gives 7.