pellman
- 683
- 6
Never mind. I got this one. Couldn't figure out how to delete the post though.
Attachments
-
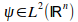 upload_2015-8-15_11-27-0.png969 bytes · Views: 567
upload_2015-8-15_11-27-0.png969 bytes · Views: 567 -
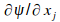 upload_2015-8-15_11-27-24.png829 bytes · Views: 574
upload_2015-8-15_11-27-24.png829 bytes · Views: 574 -
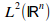 upload_2015-8-15_11-28-24.png743 bytes · Views: 575
upload_2015-8-15_11-28-24.png743 bytes · Views: 575 -
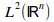 upload_2015-8-15_11-30-2.png743 bytes · Views: 549
upload_2015-8-15_11-30-2.png743 bytes · Views: 549 -
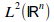 upload_2015-8-15_11-30-25.png743 bytes · Views: 569
upload_2015-8-15_11-30-25.png743 bytes · Views: 569 -
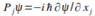 upload_2015-8-15_11-30-51.png1.1 KB · Views: 563
upload_2015-8-15_11-30-51.png1.1 KB · Views: 563
Last edited: