Gourab_chill
- 55
- 3
- Homework Statement
- I don't have much idea on what torsional constant means.
- Relevant Equations
- ω=√(C/I); here C is the torsional constant
ω'=ωβ; this formula which I saw in the solutions is related to the amplitude of the system.
The question was:
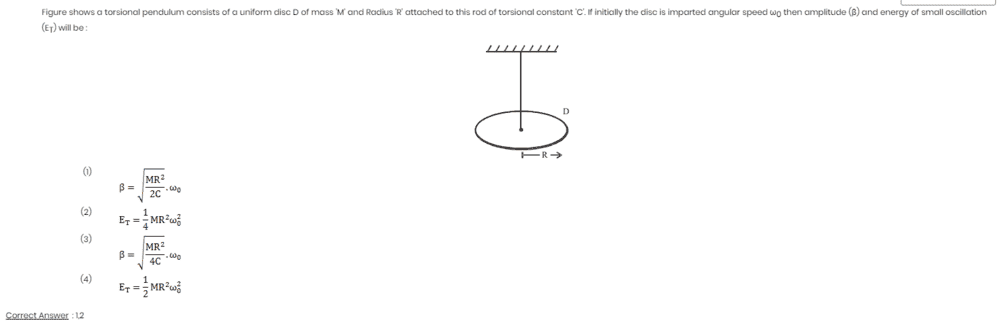
I will also include the solution:
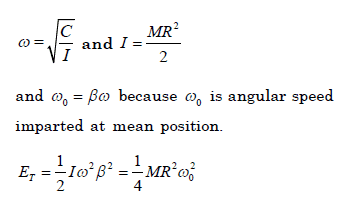
So, what is the justification of the first formula [ω=√(C/I)]? I know how to derive simple harmonic equations, this one as I guess is probably similar? But I cannot connect as to how C is used exactly.
And the second formula [ω'=ωβ], I don't know why is it used; I'm clueless about it. Can you throw some light on these topics?
I will also include the solution:
So, what is the justification of the first formula [ω=√(C/I)]? I know how to derive simple harmonic equations, this one as I guess is probably similar? But I cannot connect as to how C is used exactly.
And the second formula [ω'=ωβ], I don't know why is it used; I'm clueless about it. Can you throw some light on these topics?
Last edited by a moderator: