What is Leibniz's rule and how is it used to differentiate an integral?

[norak]

Hi, everyone, I'm new here and don't know how to type mathematics, but I have a scanner.

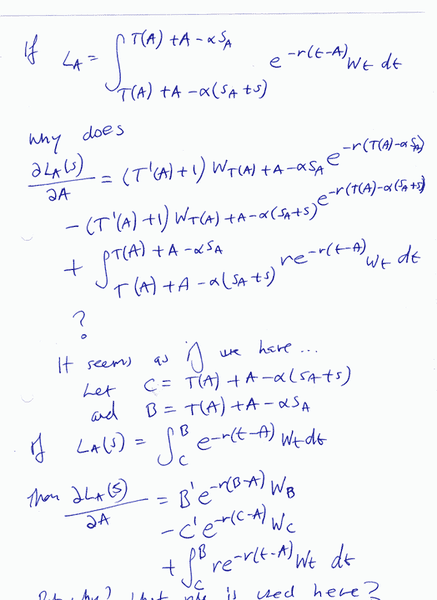
I have a function L_A and it is an integral. I want to differentiate this function with respect to A. I already have the answer written but what I don't know is how it was obtained.

Just by looking at the answer I can sort of see some sort of pattern, and I have written what I think is some sort of rule on the second half of this page, but I still don't really know what kind of differentiation rule is used here, so if any smart people here know it would greatly help me thanks!

 

[malawi_glenn]

If you first perform the whole integration, then differentiating. I.e. get an explicit expression for L_A.
What do you get then? Have you tried that?

 

[HallsofIvy]

In general, Leibniz's rule, an extension of the fundamental theorem of calculus, says:
$$\frac{\partial left(\int_{f(a,s)}^{g(a,s)} \phi(a,s,x)dx\right)}{\partial a}= \frac{\partial g}{\partial a}\phi(a,s,f(a,s))- \frac{\partial f}{\partial a}\phi(a,s,g(a,s))+ \int_{f(a,s)}^{g(a,s)} \frac{\partial \phi(a,s,x)}{da} dx$$
just the form you give. It can be derived using the fundamental theorem of calculus together with the chain rule to handle the variable limits of integration.