What is the connection between x^2 and a square shape?

[pairofstrings]

Hello.
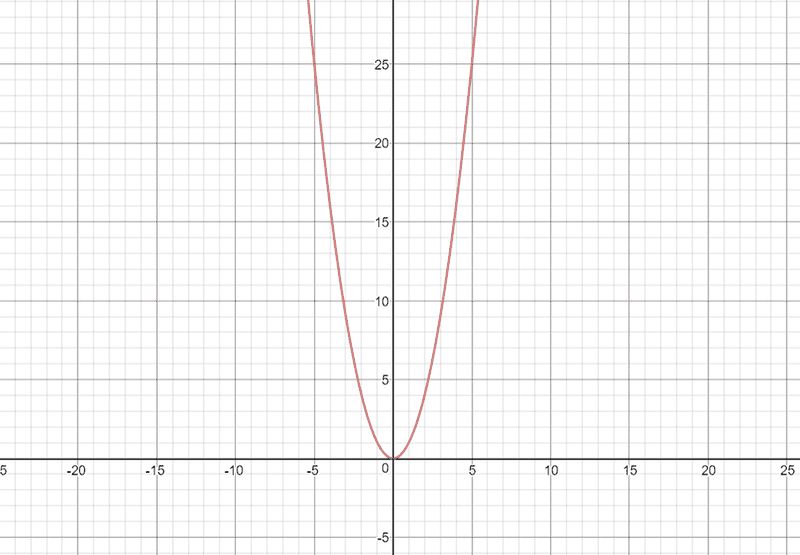
The curve y = x² is a parabola that looks like this:

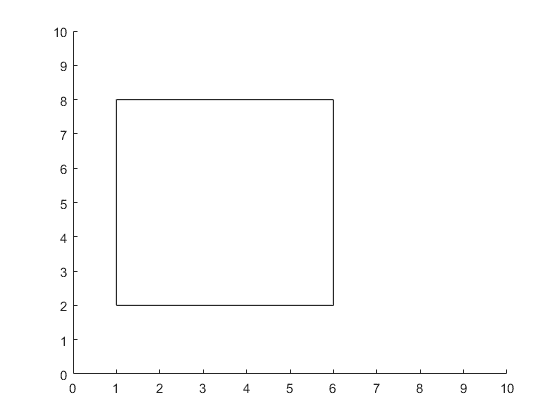
I have a shape Square that looks like this:

What I am noticing is that if I consider the equation y = x² and also the shape Square, I find that there is no connection between them but the equation y = x² is pronounced as x-square.

Can someone please clarify the link between Square shape and the equation y = x²?

Thanks!

 

[jedishrfu]

Your second diagram shows a square where the x-axis side is 6 units long and the y-axis side is 6 units long.

So the x-axis and y-axis represents length in some unit of measure like feet or meters.

Your first diagram is different in that the y-axis represents area ie feet^2 or meters^2 and so given some x units in feet or meters you can look at its y-value to get the area of a square with sides that x units long. If you look at 6 on the x-axis you will see the y value = 36 which is the area of your square.

There is nothing more to see here.

 

[jbriggs444]

I have a shape Square that looks like this:
View attachment 227977

You realize that is not a square, right? It is a five by six rectangle.

 

[jedishrfu]

You realize that is not a square, right? It is a five by six rectangle.

Good catch, I didn't see that. It could be the source of confusion ie 30 units^2 =/= 36 units^2

 

[Mark44]

$x \cdot x$ or $x^2$ (read as x squared) is the area of a square x units on a side.
$x \cdot x \cdot x$ or $x^3$ (read as x cubed) is the volume of a cube x units on a side.
For exponents 4 or higher, $x^4, x^5, \dots$ are just read as x to the fourth power, x to the fifth power, and so on.

As @jedishrfu already said, there is no direct connection between the parabola $y = x^2$ and a square, other than this function gives you the area of a square x units on a side. In the same way, the graph of $y = x^3$ gives you the volume of a cube x units on a side, but the shape of the graph does not appear as a solid figure of any kind.

 

[CWatters]

Deleted. Mark beat me to it.