What is the Cutoff Wavelength for a Photon Passing Through a Waveguide?
Click For Summary
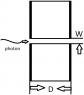
The discussion centers on determining the cutoff wavelength for a photon passing through a waveguide. It highlights that while quantum mechanics allows for a non-zero probability of photon transmission regardless of wavelength, classical electromagnetics provides a more defined cutoff based on waveguide dimensions. For a rectangular waveguide, the cutoff wavelength for the lowest modes is calculated as λ_c = 2W. However, wavelengths longer than this cutoff will experience attenuation, and the effective transmission depends on how one defines the cutoff in terms of power reduction. The conversation emphasizes the interplay between quantum behavior and classical wave propagation in waveguides.
Similar threads
- · Replies 0 ·
- · Replies 12 ·
- · Replies 5 ·
- · Replies 12 ·
- · Replies 3 ·
- · Replies 20 ·
- · Replies 2 ·
- · Replies 8 ·
- · Replies 2 ·