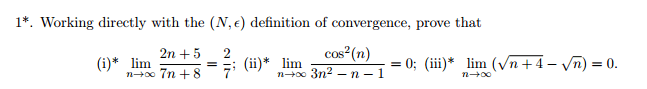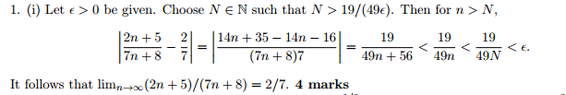What is the limit of the difference of square roots of consecutive numbers?

[amr21]

Hello,
I am struggling to understand a simple question on limits. I have watched a video trying to explain the theory and even have the answer right in front of me but I still don't understand. Could somebody please explain the steps in detail for me just for the first question as I'm hoping I'll understand the other after that.

Thank you

View attachment 5557

View attachment 5558

 

[Prove It]

Hello,
I am struggling to understand a simple question on limits. I have watched a video trying to explain the theory and even have the answer right in front of me but I still don't understand. Could somebody please explain the steps in detail for me just for the first question as I'm hoping I'll understand the other after that.

Thank you

To prove a limit to infinity, you want to have a certain tolerance for your function value $\displaystyle \begin{align*} \epsilon > 0 \end{align*}$ and show that no matter how far along you go on your x, i.e. some large value N, going any further will still ensure that your function value will always be within the tolerance away from the limiting value L. In other words, to prove $\displaystyle \begin{align*} \lim_{x \to \infty} f(x) = L \end{align*}$ you have to show that $\displaystyle \begin{align*} x > N \implies \left| f(x) - L \right| < \epsilon \end{align*} $.

So for the first one, to prove $\displaystyle \begin{align*} \lim_{n \to \infty} \frac{2\,n + 5}{7\,n + 8} = \frac{2}{7} \end{align*}$ you need to show that for any $\displaystyle \begin{align*} \epsilon > 0, \, n > N \implies \left| \frac{2\,n + 5}{7\,n + 8} - \frac{2}{7} \right| < \epsilon \end{align*}$.

Working with the second part we have

$\displaystyle \begin{align*} \left| \frac{2\,n + 5}{7\,n + 8} - \frac{2}{7} \right| &< \epsilon \\ \left| \frac{7 \,\left( 2\,n + 5 \right) }{7\,\left( 7\,n + 8 \right)} - \frac{2\,\left( 7\,n + 8 \right)}{7\,\left( 7\,n + 8 \right) } \right| &< \epsilon \\ \left| \frac{7\,\left( 2\,n + 5 \right) - 2\,\left( 7\, n + 8 \right) }{7\,\left( 7\, n + 8 \right) } \right| &< \epsilon \\ \left| \frac{14\,n + 35 - 14\,n - 16}{7\,\left( 7\, n + 8 \right) } \right| &< \epsilon \\ \left| \frac{19}{7\,\left( 7\, n + 8 \right) } \right| &< \epsilon \\ \frac{19}{7\,\left| 7\,n + 8 \right| } &< \epsilon \\ \frac{1}{\left| 7\,n + 8 \right| } &< \frac{7\,\epsilon }{19} \\ \left| 7\,n + 8 \right| &> \frac{19}{7\,\epsilon} \\ 7\,n + 8 &> \frac{19}{7\,\epsilon} \textrm{ as } n > 0 \\ 7\,n &> \frac{19}{7\,\epsilon} - 8 \\ n &> \frac{19}{\epsilon} - \frac{8}{7} \end{align*}$

So it would make sense to let $\displaystyle \begin{align*} N = \frac{19}{\epsilon} - \frac{8}{7} \end{align*}$, because then by setting $\displaystyle \begin{align*} n > N \end{align*}$ and reversing every step, we definitely do show that $\displaystyle \begin{align*} \left| \frac{2\,n + 5}{7\,n + 8} - \frac{2}{7} \right| < \epsilon \end{align*}$, and thus $\displaystyle \begin{align*} \lim_{n \to \infty} \frac{2\,n + 5}{7\,n + 8} = \frac{2}{7} \end{align*}$

 

[Prove It]

Hello,
I am struggling to understand a simple question on limits. I have watched a video trying to explain the theory and even have the answer right in front of me but I still don't understand. Could somebody please explain the steps in detail for me just for the first question as I'm hoping I'll understand the other after that.

Thank you

For (ii) I would make use of the Sandwich Theorem. We should note that for large n, $\displaystyle \begin{align*} 3\,n^2 - n - 1 > 0 \end{align*}$ and since $\displaystyle \begin{align*} 0 \leq \cos^2{(n)} \leq 1 \end{align*}$ for all real n, that means $\displaystyle \begin{align*} 0 \leq \frac{\cos^2{(n)}}{3\,n^2 - n - 1 } \leq \frac{1}{3\,n^2 - n - 1} \end{align*}$ for large n.

That means if we can show $\displaystyle \begin{align*} \lim_{n \to \infty} \frac{1}{3\,n^2 - n - 1} = 0 \end{align*}$, that means as $\displaystyle \begin{align*} \frac{\cos^2{(n)}}{3\,n^2 - n - 1} \end{align*}$ is sandwiched between 0's, it too must have a limit of 0.

So to prove $\displaystyle \begin{align*} \lim_{n \to \infty} \frac{1}{3\,n^2 - n - 1} = 0 \end{align*}$ we need to show for all $\displaystyle \begin{align*} \epsilon > 0, \, n > N \implies \left| \frac{1}{3\,n^2 - n - 1} - 0 \right| < \epsilon \end{align*}$. Do you think you could have a go of this?

- - - Updated - - -

Hello,
I am struggling to understand a simple question on limits. I have watched a video trying to explain the theory and even have the answer right in front of me but I still don't understand. Could somebody please explain the steps in detail for me just for the first question as I'm hoping I'll understand the other after that.

Thank you

For (iii) I would first write:

$\displaystyle \begin{align*} \sqrt{n + 4} - \sqrt{n} &\equiv \frac{\left( \sqrt{n + 4} - \sqrt{n} \right) \left( \sqrt{n + 4} + \sqrt{n} \right) }{\sqrt{n + 4} + \sqrt{n}} \\ &\equiv \frac{n + 4 - n}{\sqrt{n + 4} + \sqrt{n}} \\ &\equiv \frac{4}{\sqrt{n + 4} + \sqrt{n}} \end{align*}$

Do you think you can have a go of showing for all $\displaystyle \begin{align*} \epsilon > 0 , \, n > N \implies \left| \frac{4}{\sqrt{n+4} + \sqrt{n}} - 0 \right| < \epsilon \end{align*}$?