What is the Low Frequency Gain of a Circuit?

[NHLspl09]

I have started working on a summer assignment for my Fall semester EE course and was given a gain problem with an op amp (Problem shown below - EE P3.1). My professor also gave me, what he calls, 'Typical Homework Solutions.' I have based most of my work with the example problem he gave us(Attatchment EE P3.2), but have come to a dead end in my work...

Homework Statement

(Attatchment below - EE P3.1)
Determine the transfer function of the circuit given.

Homework Equations

V_n(t) = V_p(t)
V_p(t) = V_i(t)
V_n(t) = V_p(t) = V_i(t)

The Attempt at a Solution

(Attatchment below - EE P3)

0 = (G₁ + C₁s)V_i(t) + G₂[V_i(t) - V_o(t)]

The thing that doesn't seem right is (looking at EE P3) that if I were to bring the V_i(t) over to the right of the equation so it is V_o(t)/V_i(t), the gain would then be ((G₁ + C₁s)+G₂)/(G₂) and that just does not seem like the correct answer... Any ideas/input as to if I'm just wrong in thinking that is not right?

 

[donpacino]

ok you want to do nodal analysis. in an ideal op-amp with high gain negative feedback the negative input is equel to the positive input. so the equation is.

vi/(r1+1/c1)+(vi-vo)/(r2)=0

note that i did not convert to s yet. you are supposed to convert to s first however i havnt done this problem yet

when you convert to s i think all that happens is the 1/c1 becomes 1/(sc1)

ps. guess who i am

 

[MisterX]

vi/(r1+1/c1)+(vi-vo)/(r2)=0

when you convert to s i think all that happens is the 1/c1 becomes 1/(sc1)

It is wrong to write the impedance of a capacitor 1/c1 and then "convert to s." It is not correct to write the impedance of a capacitor as 1/c1, generally.

 

[donpacino]

then how would you do it? don't criticize if you can't show me a better answer

 

[MisterX]

The first equation I would write would be in the s domain.
something like:
$\frac{V_{i}}{R_{1} + \frac{1}{C_{1}s}} =\frac{V_{o} - V_{i}}{R_{2}}$

where V_i and V_o are the Laplace transforms of v_i(t) and v_o(t), respectively.

This is much like what you wrote, except without the incorrect "1/c1".

 

[NHLspl09]

ps. guess who i am

Hahah hi Leo

The first equation I would write would be in the s domain.
something like:
$\frac{V_{i}}{R_{1} + \frac{1}{C_{1}s}} =\frac{V_{o} - V_{i}}{R_{2}}$

where V_i and V_o are the Laplace transforms of v_i(t) and v_o(t), respectively.

This is much like what you wrote, except without the incorrect "1/c1".

I understand where you're coming from.. But when you do this I don't quite understand how you algebraically have an end result of $\frac{V_{o}}{V_{i}}$.. Any advice on this?

 

[gneill]

I understand where you're coming from.. But when you do this I don't quite understand how you algebraically have an end result of $\frac{V_{o}}{V_{i}}$.. Any advice on this?

Cross multiply, expand each side and collect like terms (v_o's and v_i's)... the usual algebraic dance

 

[NHLspl09]

Cross multiply, expand each side and collect like terms (v_o's and v_i's)... the usual algebraic dance

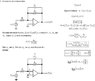
Haha wow I feel stupid for not seeing that... I worked it out and found a gain shown in the attatchment below. Does this gain seem correct? I also "attempted" in putting it in the form the professor asked for.. and I think that went miserably wrong..

 

[gneill]

Your algebra is a bit "exotic"

Try this:
$$\frac{v_i}{R_1 + \frac{1}{s C_1}} = \frac{v_o - v_i}{R_2}$$
Cross multiplying:
$$v_i R_2 = (v_o - v_i)\left(R_1 + \frac{1}{s C_1}\right)$$
Now separate the v terms and proceed.

 

[NHLspl09]

Your algebra is a bit "exotic"

Try this:
$$\frac{v_i}{R_1 + \frac{1}{s C_1}} = \frac{v_o - v_i}{R_2}$$
Cross multiplying:
$$v_i R_2 = (v_o - v_i)\left(R_1 + \frac{1}{s C_1}\right)$$
Now separate the v terms and proceed.

Haha I did do this, maybe I didn't show it very well. I did what you showed, then brought the v_i over to produce the gain and cancel out a set of v_i's, which = -1. I then took the 1 and added it to the left side of the equation. Does this make it more clear?

 

[gneill]

$$v_i R_2 = (v_o - v_i)\left(R_1 + \frac{1}{s C_1}\right)$$
$$v_i (R_2 + R_1 + \frac{1}{s C_1}) = v_o \left(R_1 + \frac{1}{s C_1}\right)$$
$$\frac{v_o}{v_i} = \frac{(R_2 + R_1 + \frac{1}{s C_1})}{\left(R_1 + \frac{1}{s C_1}\right)}$$
[STRIKE]Now pull R₁ + R₂ out of the numerator, and R₁ out of the denominator. Proceed.[/STRIKE]

EDIT: Better idea: multiply numerator and denominator by sC₁.

 

[NHLspl09]

$$v_i R_2 = (v_o - v_i)\left(R_1 + \frac{1}{s C_1}\right)$$
$$v_i (R_2 + R_1 + \frac{1}{s C_1}) = v_o \left(R_1 + \frac{1}{s C_1}\right)$$
$$\frac{v_o}{v_i} = \frac{(R_2 + R_1 + \frac{1}{s C_1})}{\left(R_1 + \frac{1}{s C_1}\right)}$$
[STRIKE]Now pull R₁ + R₂ out of the numerator, and R₁ out of the denominator. Proceed.[/STRIKE]

EDIT: Better idea: multiply numerator and denominator by sC₁.

Gotcha, it may be a silly question.. but by doing so would it not cancel out the sC₁ in the numerator and denomenator?

 

[gneill]

Gotcha, it may be a silly question.. but by doing so would it not cancel out the sC₁ in the numerator and denomenator?

Not quite, it has the effect of turning the 1/sC1 terms into 1's, and turning the resistance terms into s*R*C type terms... otherwise known as s/ω type terms...

 

[NHLspl09]

Not quite, it has the effect of turning the 1/sC1 terms into 1's, and turning the resistance terms into s*R*C type terms... otherwise known as s/ω type terms...

I did not realize that was the the actual term s/ω, which is what form the professor asks for the answer to be in. So s*R*C is equivilent to s/ω?

 

[gneill]

I did not realize that was the the actual term s/ω, which is what form the professor asks for the answer to be in. So s*R*C is equivilent to s/ω?

Yup. The units of R*C yield seconds. 1/seconds yields a frequency...

 

[NHLspl09]

Yup. The units of R*C yield seconds. 1/seconds yields a frequency...

From what you have said, I found a gain and found ω_z & ω_p (shown in attatchment), although what doesn't make sense to me is that there is no A_LF.. my thoughts were that (where I circled and labeled 1) there were missing parentheses and the R₂ should be A_LF?? I could be wrong and just not understanding this problem at all

 

[gneill]

The frequency terms have form s/ω (the ω's themselves do not contain s), so you should have

$w_z = 1/((R_1 + R_2)*C_1)$

$w_p = 1/(R_1*C_1)$

A low frequency gain of unity, $A_{LF} = 1$, should be perfectly acceptable.

 

[NHLspl09]

The frequency terms have form s/ω (the ω's themselves do not contain s), so you should have

$w_z = 1/((R_1 + R_2)*C_1)$

$w_p = 1/(R_1*C_1)$

A low frequency gain of unity, $A_{LF} = 1$, should be perfectly acceptable.

Ok ok I now see what you mean and understand it a lot better. I needed to keep going and factor out the s from both the ω_z & ω_p, which then gives me an end result of ω_z = $1/((R_1 + R_2)*C_1)$ & ω_p = $1/(R_1*C_1)$, exactly what you got which is great!

I understand how I got a low frequency of 1, I just don't really understand the purpose/information on the actual term low frequency gain.. If that makes sense

 

[gneill]

The low frequency gain tells you what the circuit gain will be when the input signal is of very low frequency (DC or approaching DC). So if, for example, the input signal happened to be a 1V DC value, the output would settle at 1V also.

 

[NHLspl09]

The low frequency gain tells you what the circuit gain will be when the input signal is of very low frequency (DC or approaching DC). So if, for example, the input signal happened to be a 1V DC value, the output would settle at 1V also.

Ahh alright now I understand this better than before and understand the problem. Thank you for all of your help/input and explanations! They are greatly appreciated and very helpful!