How can I analyze this transimpedance amplifier?

[Boltzman Oscillation]

Homework Statement

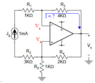
The opAmp network shown in figure 68 is a transimpedance amplifer that employs both negative and positive feedback. Assuming that the op-amp is ideal, calculate the value for the output voltage for Jg is 1mA.The circuit and question are this:

https://www.chegg.com/homework-help/questions-and-answers/84-op-amp-network-shown-figure-84-transimpedance-amplifier-employs-negative-positive-feedb-q31684479

Homework Equations

Vp = Vn
In = Ip = 0
KCL
KVL

The Attempt at a Solution

I tried using KCL to make the following

(Vn - Vj)/R1 + (Vn-Vo)/R2 = 0

(Vn - Vj)/ R3 + Vn/R5 + (Vn - Vo)/R4 = 0

but I really don't think this is the way to solve the problem. I don't really know the voltage across the current source so it's pretty useless for me to use it here. Can anyone guide me to the right direction? Does anyone know a good resource to read on op amps?

 

[willem2]

I tried using KCL to make the following

(Vn - Vj)/R1 + (Vn-Vo)/R2 = 0

(Vn - Vj)/ R3 + Vn/R5 + (Vn - Vo)/R4 = 0

but I really don't think this is the way to solve the problem. I don't really know the voltage across the current source so it's pretty useless for me to use it here. Can anyone guide me to the right direction? Does anyone know a good resource to read on op amps?

I think you used KCL correctly.. Finding the current through J_g is easier than you think it is.

 

[Boltzman Oscillation]

I think you used KCL correctly.. Finding the current through J_g is easier than you think it is.

You mean the voltage? I am given the current of Jg to be 1mA but not the voltage across Jg (which is what i need if I were to use KCL.

 

[gneill]

What can you say about the current through $R_2$? Can you find an expression relating $V_o$ and the potential at the op-amp inputs?

 

[willem2]

You mean the voltage? I am given the current of Jg to be 1mA but not the voltage across Jg (which is what i need if I were to use KCL.

It certainly appears you are trying to use the fact that the total current into the node at the negative input of the op-amp must be 0 when you write
(Vn - Vj)/R1 + (Vn-Vo)/R2 = 0. It's Kirchhof's Current law, you know what the current is through R1.

Trick Question. What is the difference between a current source, and the same current source in series with a 5k resistor?

 

[Boltzman Oscillation]

It certainly appears you are trying to use the fact that the total current into the node at the negative input of the op-amp must be 0 when you write
(Vn - Vj)/R1 + (Vn-Vo)/R2 = 0. It's Kirchhof's Current law, you know what the current is through R1.

Trick Question. What is the difference between a current source, and the same current source in series with a 5k resistor?

I don't know? A current source in series with a resistor can be transformed to a voltage sorce with a resistance in parallel.

 

[Boltzman Oscillation]

What can you say about the current through $R_2$? Can you find an expression relating $V_o$ and the potential at the op-amp inputs?

View attachment 234634

Yes i can do that and I've actually done it in my notes but i will still end up with a variable for the voltage of Jg in my equation. Do i not have to take that out somehow?

 

[gneill]

I don't know? A current source in series with a resistor can be transformed to a voltage sorce with a resistance in parallel.

Nope. You can transform a voltage source with a series resistance into a current source with a parallel resistance. And you can transform a current source with a parallel resistance into a voltage source with a series resistance. But you cannot transorm a current source with a series resistance into anything that doesn't look like a current source. Same goes for a voltage source in parallel with a resistor.

Think about it. If you place a resistor across a voltage source V, what voltage will you measure across the source? Can any resistor value change it?

Now think about the current source with a series resistor...

Yes i can do that and I've actually done it in my notes but i will still end up with a variable for the voltage of Jg in my equation. Do i not have to take that out somehow?

You'r doing KCL and so summing currents. What current is coming from Jg?

 

[Boltzman Oscillation]

Nope. You can transform a voltage source with a series resistance into a current source with a parallel resistance. And you can transform a current source with a parallel resistance into a voltage source with a series resistance. But you cannot transorm a current source with a series resistance into anything that doesn't look like a current source. Same goes for a voltage source in parallel with a resistor.

Think about it. If you place a resistor across a voltage source V, what voltage will you measure across the source? Can any resistor value change it?

Now think about the current source with a series resistor...

You'r doing KCL and so summing currents. What current is coming from Jg?

Oh so one of my equations should be:

-Jg + In + Ir2 = 0

this is because the current through R1 is the same as the current source? This would give me:

-Jg + (Vn - Vo)/R2 = 0 (1)

(Vn - V3)/R3 + Vn/R5 + (Vn - Vo)/R4 (2)

I can then transform equation one to:

-Jg/R2 + Vn/R2 = Vo (3)

Which can be plugged into (2)? Am I doing this right?

 

[gneill]

Oh so one of my equations should be:

-Jg + In + Ir2 = 0

this is because the current through R1 is the same as the current source?

Yes. No matter what resistance is placed in the path of an ideal current source, the same current flows.

This would give me:

-Jg + (Vn - Vo)/R2 = 0 (1)

(Vn - V3)/R3 + Vn/R5 + (Vn - Vo)/R4 (2)

I can then transform equation one to:

-Jg/R2 + Vn/R2 = Vo (3)

Which can be plugged into (2)? Am I doing this right?

I don't see where V3 comes from. When you do KCL at the bottom node, what current is Jg pulling from that node?

 

[Boltzman Oscillation]

Yes. No matter what resistance is placed in the path of an ideal current source, the same current flows.

I don't see where V3 comes from. When you do KCL at the bottom node, what current is Jg pulling from that node?

Sorry I misread my solution.

I believe the current across R3 should be Jg right? So equation 2 should become:

Jg + Vn/R5 + (Vn -Vo)/R4 = 0

 

[gneill]

That looks better, yes.

 

[Boltzman Oscillation]

Nope. You can transform a voltage source with a series resistance into a current source with a parallel resistance. And you can transform a current source with a parallel resistance into a voltage source with a series resistance. But you cannot transorm a current source with a series resistance into anything that doesn't look like a current source. Same goes for a voltage source in parallel with a resistor.

Think about it. If you place a resistor across a voltage source V, what voltage will you measure across the source? Can any resistor value change it?

Now think about the current source with a series resistor...

You'r doing KCL and so summing currents. What current is coming from Jg?

I understand now, a resistance in series with a current source will have a current value of that current source. I can look at this by visualizing the ideal current source.

 

[Boltzman Oscillation]

Okay i think I have the right tools to complete this question. Thank you all.