Homework Help Overview
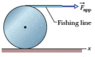
The discussion revolves around determining the magnitude of the acceleration of the center of mass of a uniform solid cylinder subjected to a constant horizontal force. The problem involves concepts from dynamics, specifically relating to torque and the motion of rigid bodies.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Problem interpretation
Approaches and Questions Raised
- Participants explore the use of torque to analyze the forces acting on the cylinder, with one participant expressing confusion about the application of torque and attempting to set up the equations. Others suggest using the parallel axis theorem and applying Newton's equations to eliminate frictional forces.
Discussion Status
The discussion is active, with participants questioning the setup of the torque equation and clarifying concepts such as the parallel axis theorem. There is a focus on understanding the forces at play and how they contribute to the net torque acting on the cylinder.
Contextual Notes
Participants are navigating the complexities of the problem, including the roles of different forces and torques, and there is an emphasis on ensuring clarity in the equations being used. The original poster expresses confusion about the approach, indicating a need for further exploration of the concepts involved.