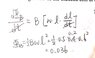What is the magnitude of the induced EMF?

[hidemi]

Homework Statement

A rectangular wire loop (length = 60 cm, width = 40 cm) lies completely within a perpendicular and uniform magnetic field of magnitude of 0.5 T. If the length of the loop starts increasing at a rate of 20 mm/s at time t= 0, while the width is decreasing at the same rate, what is the magnitude of the inducede mf at time t= 4.0 s?
a.6.8 mV
b.5.2 mV
c.3.6 mV
d.8.4 mV
e.10 mV

Answer: C

Relevant Equations

dΦB/dt = dB/dt*A

I did the question in this way as attached. I got the crrect answer, but I feel unsure if it is the right way of doing it.

 

[rsk]

According to your equation there, Emf depends on the rate of change of flux, not on the flux itself.

So, where is the rate of change greatest? It helps to picture the sin or cos graph.

 

[hidemi]

According to your equation there, Emf depends on the rate of change of flux, not on the flux itself.

So, where is the rate of change greatest? It helps to picture the sin or cos graph.

I typed the wrong question. I just edited and saved the question just now, could you read it again? thanks

 

[Gordianus]

I'd suggest you first compute the flux and later on, the derivative. You've made a mistake.

 

[Steve4Physics]

Relevant Equations:: dΦB/dt = dB/dt*A

You mean dΦ/dt = dB/dt*A. This applies when B is changing and A is constant. But in this question B is constant and A changing. So the equation is irrelevant.

Try working through these steps.

1. Write an equation for the length (in metres) as a function of time (in seconds).

2. Similarly for width.

3. Using the above, write an expression for the area (in square metres) as a function of time.

4. Since the field is perpendicular to the plane of the loop $\phi = BA$. Write an expression for $\frac {d\Phi}{dt}$ assuming both B and A are functions of time (use the product rule).

In this question B is constant and A is a function of time. So what is $\frac {d\Phi}{dt}$?

See if you can take it from there.

 

[hidemi]

You mean dΦ/dt = dB/dt*A. This applies when B is changing and A is constant. But in this question B is constant and A changing. So the equation is irrelevant.

Try working through these steps.

1. Write an equation for the length (in metres) as a function of time (in seconds).

2. Similarly for width.

3. Using the above, write an expression for the area (in square metres) as a function of time.

4. Since the field is perpendicular to the plane of the loop $\phi = BA$. Write an expression for $\frac {d\Phi}{dt}$ assuming both B and A are functions of time (use the product rule).

In this question B is constant and A is a function of time. So what is $\frac {d\Phi}{dt}$?

See if you can take it from there.

I got it. Thank you so much.