vanhees71 said:
What irks me is when for some irrational "philosophical" reasons elementary observable facts, which don't need any vaguely defined interpretational notions, are denied. The claim that the conservation laws are "valid only on average" has been refuted by Bothe et al already about 100 years ago!
Otherwise it's clear that entanglement and particularly its experimental realization is intriguing, but it only seems "weird", because we are not used to quantum phenomena in everyday life. For me, scientific theories are descriptions of what can be objectively and quantitatively observed, and QT is very successful with that, including the correlations due to entanglement, and that's thus very well understood.
Let me try again, since this is directly relevant to the OP. "Average-only" conservation, which is a mathematical fact about Bell states, seems to be confusing vanhees71, so I'll go straight to the source of that fact, i.e., "average-only" projection aka Information Invariance & Continuity aka superposition aka spin aka the qubit aka ... . What I'm presenting next will probably not make any sense to those who haven't taken QM. That's good, it will make my point all the better. For those readers, just read the words and gloss right over the mathematics. No worries, I'll follow the Hilbert space formalism with a conceptual explanation that you can (probably) understand. That's the point of this exercise.
Suppose I make a measurement on a spin up state along the z axis. We might do that physically by sending a beam of silver atoms through a pair of Stern-Gerlach (SG) magnets aligned along what we call the z axis. Then we direct the atoms that are deflected upwards out of those SG magnets through another pair of SG magnets oriented at ##\hat{b}## making a an angle ##\theta## with respect to ##\hat{z}## (figure below). How does QM describe the outcomes of that measurement at ##\hat{b}##?
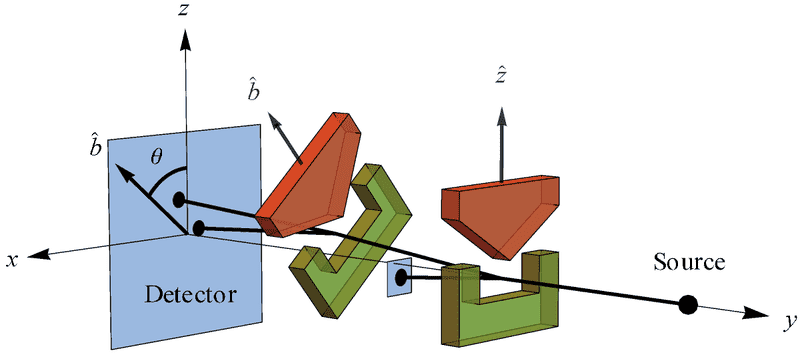
The state being measured is ##|\psi\rangle = |z+\rangle## and there are two possible outcomes of our measurement that I will call +1 (deflected towards red pole of SG magnets) denoted by ##|+\rangle## and -1 (deflected towards green pole of SG magnets) denoted by ##|-\rangle##. The Hilbert space formalism says the probability of getting the +1 outcome is ##|\langle+|\psi\rangle|^2 = \cos^2{\left(\frac{\theta}{2}\right)}## and the probability of getting the -1 outcome is ##|\langle-|\psi\rangle|^2 = \sin^2{\left(\frac{\theta}{2}\right)}## (Born rule). These are just the squares of the projection of ##|\psi\rangle = |z+\rangle## onto the two eigenvectors of our measurement operator ##\sigma## given by ##\sigma = \hat{b}\cdot\vec{\sigma}=b_x\sigma_x + b_y\sigma_y + b_z\sigma_z## where ##\sigma_x##, ##\sigma_y##, ##\sigma_z## are the Pauli matrices. The average is then given by the expectation value of ##\sigma## for ##|\psi\rangle##, i.e.,
##\langle\sigma\rangle := \langle \psi| \sigma|\psi \rangle = \cos{(\theta)}##
All of that is standard textbook QM. For physicists like vanhees71 this constitutes "understanding":
For me, scientific theories are descriptions of what can be objectively and quantitatively observed, and QT is very successful with that, including the correlations due to entanglement, and that's thus very well understood.
However, if you who are not familiar with standard textbook QM, this quote by Chris Fuchs might resonant with you:
Associated with each system [in quantum mechanics] is a complex vector space. Vectors, tensor products, all of these things. Compare that to one of our other great physical theories, special relativity. One could make the statement of it in terms of some very crisp and clear physical principles: The speed of light is constant in all inertial frames, and the laws of physics are the same in all inertial frames. And it struck me that if we couldn’t take the structure of quantum theory and change it from this very overt mathematical speak—something that didn’t look to have much physical content at all, in a way that anyone could identify with some kind of physical principle—if we couldn’t turn that into something like this, then the debate would go on forever and ever. And it seemed like a worthwhile exercise to try to reduce the mathematical structure of quantum mechanics to some crisp physical statements.
That's what Gell-Mann, Feynman, and Mermin were talking about in their quotes I posted earlier. All of these people are very familiar with the textbook QM formalism, so what they mean by "understanding QM" goes beyond the mere formalism.
In response to this challenge by Fuchs, Hardy (and subsequently many others) are trying to "reconstruct" QM using principles rather than the pure math a la above. They chose principles from information theory while treating QM as a "general" probability theory. Luckily, we don't have to understand their reconstructions in detail, all we need is one part of what they discovered and we can understand that conceptually.
What they found originated with the first such "axiomatic reconstruction of QM based on information-theoretic principles" published by Hardy in 2001,
Quantum Theory from Five Reasonable Axioms. What Hardy discovered was that by deleting one word ("continuous") from his fifth axiom, he would have classical probability theory instead of quantum probability theory. Thus, this quote from Koberinski and Mueller in an earlier post:
We suggest that (continuous) reversibility may be the postulate which comes closest to being a candidate for a glimpse on the genuinely physical kernel of ``quantum reality''. Even though Fuchs may want to set a higher threshold for a ``glimpse of quantum reality'', this postulate is quite surprising from the point of view of classical physics: when we have a discrete system that can be in a finite number of perfectly distinguishable alternatives, then one would classically expect that reversible evolution must be discrete too. For example, a single bit can only ever be flipped, which is a discrete indivisible operation. Not so in quantum theory: the state |0> of a qubit can be continuously-reversibly ``moved over'' to the state |1>. For people without knowledge of quantum theory (but of classical information theory), this may appear as surprising or ``paradoxical'' as Einstein's light postulate sounds to people without knowledge of relativity.
Now let me use what they discovered about "continuity", plus the relativity principle, to provide what Fuchs and others see as missing in the math above concerning spin measurements. Of course, there is more to QM, but I'm focusing here on the OP and vanhees71's confusion.
The classical probability theory we're comparing to quantum probability theory has to do with the "classical bit," which can be instantiated many ways physically, but for simplicity let's just look at two boxes and one ball. I have two measurement options, I can open box 1 or I can open box 2. I have two possible outcomes for each measurement, +1 meaning it contains a ball or -1 meaning it doesn't contain a ball. [Sometimes people use +1 and 0, as in the K-M quote, thinking of 1's and 0's for a computer, for example. I'll stick to +1 and -1 here for reasons that will be clear later.] Since the ball is in one of the two boxes, the probability that it is in box 1 plus the probability that it is in box 2 must equal 100%, i.e., ##p_1 + p_2 = 1##. So, we can represent the probability space as a line connecting the fact that the ball is in box 2 (##p_2 = 1##) and the fact that the ball is in box 1 (##p_1 = 1##) (figure below).
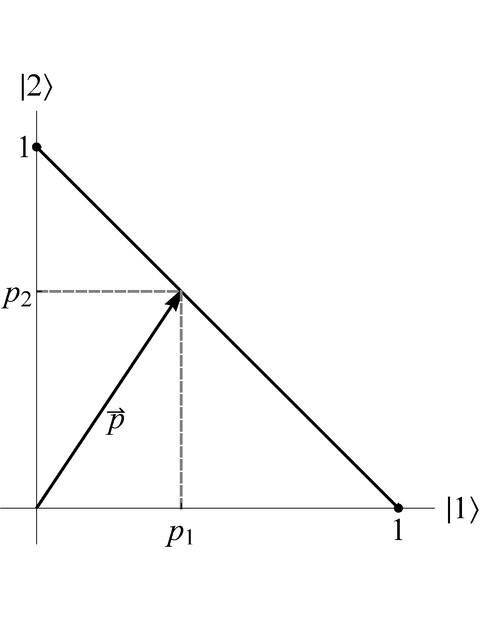
The key feature of this probability pointed out by Hardy (and employed in many reconstructions since) is that there are only two actual measurements represented in the probability space for the classical bit depicted here, i.e., those along each axis. The points along the line connecting those two "pure states" are "mixtures", they don't actually represent a measurement because you can't open a box "between" boxes 1 and 2.
In contrast, the quantum version of a bit ("qubit") allows for pure states to be connected in continuous fashion by other pure states. Here is Brukner and Zeilinger's picture of the qubit for our QM formalism above:
As you can see, we are allowed to rotate our SG magnets for our ##\sigma## measurement of ##|\psi\rangle## and we have a measurement at every ##\theta## in continuous fashion, always obtaining one of two outcomes, +1 or -1. To relate this to typical QM terminology, this is superposition per the qubit representing spin. To relate this to the information-theoretic terminology, this is Information Invariance & Continuity per Brukner and Zeilinger:
The total information of one bit is invariant under a continuous change between different complete sets of mutually complementary measurements.
where the "mutually complementary spin measurements" here are the orthogonal set for each ##\theta## as shown in this figure
Now let's finish this conceptual understanding of Information Invariance & Continuity aka spin aka the qubit by looking at what makes the difference between the qubit and classical bit "weird." I'll characterize that "weird" empirical fact by "average-only" projection, justify it by the relativity principle, and we're done!
If we were to try to understand what is going on with our spin example above, we might suppose that the silver atoms are tiny magnetic dipoles being deflected by the SG magnetic field. If that is the case, we expect the amount of deflection to vary depending on how the atoms are oriented relative to the SG magnet field as they enter it. Here is a figure from Knight's intro physics text for that "classical" picture:
The problem with this picture is of course that we only ever get two deflections, i.e., up or down, relative to the SG magnets. Even when we chose a specific case ##|\psi\rangle = |z+\rangle## and measured at ##\hat{b}## we still always got +1 or -1, no fractions (again, look at qubit picture). What we expected per our classical model would be a fractional deflection along ##\hat{b}## like this:
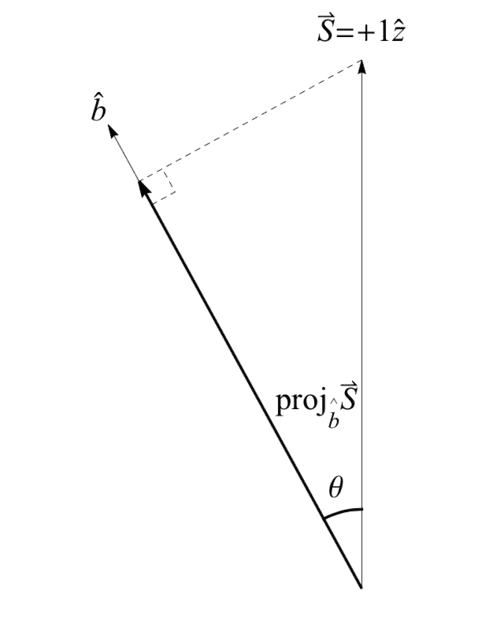
But, guess what that projection equals ... ##\cos{\theta}## ... exactly what QM gives as the average of the +1 and -1 outcomes overall, ##\langle \sigma \rangle##. And, if you start with this expectation for ##\sigma##, you can derive the ##\cos^2{\left(\frac{\theta}{2}\right)}## and ##\sin^2{\left(\frac{\theta}{2}\right)}## probabilities by requiring additionally that the probabilities add to 1 (called "normalization"). Notice that since we can only ever get +1 or -1, no fractions, we cannot ever measure ##\cos{\theta}## directly. That is to say, the projected value can only obtain on average. This means the standard textbook formalism of QM for the spin qubit can be characterized as "average-only" projection. Thus, the probabilities of our Hilbert space mathematics can be understood to follow from "average-only" projection, which is an empirical fact.
Again, we haven't introduced any interpretations or opinions or proposals here. We're simply characterizing the QM formalism conceptually. And, "average-only" conservation is exactly the same, we just replace the counterfactual ##\hat{b} = \hat{z}## measurement outcome for Bob's single qubit experiment here with the counterfactual ##\hat{b} = \hat{a}## measurement outcome (required for conservation of spin angular momentum) for Bob when Alice measures at ##\hat{a}##. In other words, "average-only" conservation for Bell state qubits results from "average-only" projection for single qubits. This is not an interpretation.
To conclude, as Weinberg pointed out, we are measuring Planck's constant h when we do our spin measurement. And, we are in different reference frames related by spatial rotations as we vary ##\theta## (per Brukner and Zeilinger). So, Information Invariance & Continuity entails everyone will measure the same value for h (##\pm##) regardless of their reference frame orientation relative to the source ("Planck postulate" -- an empirical fact equivalent to the light postulate of SR: everyone will measure the same value for c regardless of their reference frame motion relative to the source). Both are simply statements of empirical facts. Thus, everything presented to this point constitutes a collection of empirical and mathematical facts per standard textbook QM.
Finally, we give a principle account of the mathematical facts following from the empirical fact a la Einstein for SR. That is, we justify the "Planck postulate" by the relativity principle. Just as time dilation and length contraction follow mathematically from the light postulate which is justified by the relativity principle, the qubit probabilities (whence "average-only" conservation) follow mathematically from the Planck postulate which is justified by the relativity principle. This last step is indeed a proposal, but it's as solid as what Einstein did for SR :-)