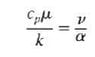What Is the Physical Interpretation of Prandtl Number in Heat Transfer?

[Sahil Dev]

Homework Statement

Physical meaning of Prandtl number

Homework Equations

See attached image

The Attempt at a Solution

I have been reading about the boundary layer cocept whilst doing a self study on heat tarsnfer.

I have come across the diemnsionless numbers: Reynolds number, Prandtl number, Nusselt number.

I have a question cocnerning Prandtl number- its physical interpretation and would like to know if I'm right here.

The text says;
· The physical interpretation of Prandtl number follows from its definition as a ratio of the momentum diffusivity to the thermal diffusivity.
· It is a measure of relative effectiveness of momentum and energy transport by diffusion in the velocity and thermal boundary layers, respectively.

Am I right in interpreting;

Prandtl number is the ratio of heat ttarnsferred through convection to the heat tarsnferred through conduction.

That is: consdering an example, of flow of fluid over a flat plate (see attached image- velocity_boundary_layer.jpg), at the region where the fluid is in contact with the plate, heat tarnsfer is through pure conduction- since the fluid velocity is '0' here) whereas above (within the boundary later thickness) heat transfer will be through convection as well.

Please can anyone help me with my intepretation as I'm myself not very cmfortable with it.

Thanks
Sahil

 

[Chestermiller]

I think you are spending too much time trying to ascribe some physical significance to Pr. My advice is just to accept that it is equal to the ratio of the kinematic viscosity to the thermal diffusivity, and move on. But pay attention to how it comes into play in actual heat transfer situations that you study such as in fully developed laminar flow heat transfer in a tube or, as you've shown, heat transfer to a fluid in flow over a flat plate.

At high Pr (like liquids), the thermal boundary layer lies inside the velocity boundary layer, but at very low Pr, the thermal boundary exceeds the velocity boundary layer in thickness.

Chet