Nano-Passion
- 1,291
- 0
I just learned the proof for the Pythagorean theorem.. my mind was blown! =D Simply amazing.
Nano-Passion said: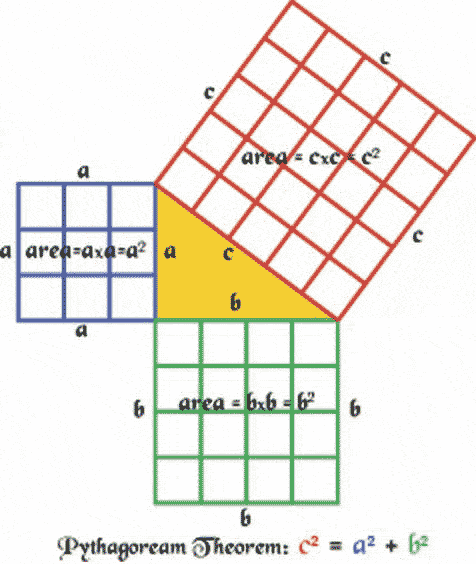
I liked this one particularly, the one in the post above is pretty awesome too.
DarthPickley said:Well, that one you mention isn't really a proof at all, it just sort of shows that it works for the case of a triangle with side lengths of 3, 4, and 5.
Nano-Passion said:Are you sure? It works for any right angle triangle. And the Pythagorean theorem works only for right angle triangles. So?
Nano-Passion said:Are you sure? It works for any right angle triangle. And the Pythagorean theorem works only for right angle triangles. So?
gb7nash said:I really like the geometric proof. The first time I saw it I stared at it for a long time.