What is the purpose of the Einstein stress-energy tensor?

[AleksanderPhy]

Hello I'm new here on this forum and on physics too.
I have problem on Einstein famous equation

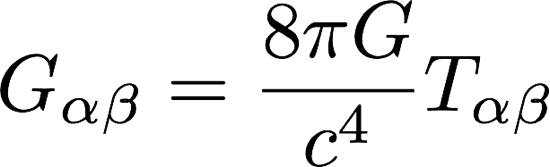
I have a problem on the last component Tαβ I know that tensor name is Einstein stress-energy tensor and I know that Tαβ is:https://qph.is.quoracdn.net/main-qimg-c810f8bca07c6e580138cc1906a693bf?convert_to_webp=true but can we describe it some other versions not like matrics version

 

[andrewkirk]

The stress-energy tensor is a way of representing the more familiar notions of mass-energy and momentum in a way that is independent of reference frame - ie the coordinate system used. It's easy enough to see that traditional measurements of momentum are coordinate dependent - they vary between reference frames. It is less obvious, but nevertheless true, that measurements of mass-energy also depend on reference frame.

Einstein's gravity equation is designed to express the dependence of the curvature of spacetime on some measure of mass-energy. But since the curvature is coordinate-free, the measure of mass-energy needs to be coordinate-free too. The stress-energy tensor is that coordinate-free 'object'.

The matrix you have written above is a representation of the tensor in coordinates. But note it is the representation that uses coordinates, and is coordinate-dependent, not the tensor itself. That is, the 4 x 4 matrix is not the tensor but a representation of it. Although one sometimes relaxes one's precision and refers to the matrix as a tensor.

Mathematically, the tensor is a function that takes two vectors as inputs and gives a real scalar as output. You can if you wish think of the first vector as answering the question 'what do you want to measure?' (to which the answer will be something like 'energy, x-momentum, y-momentum or z-momentum' or a combination thereof) and the second vector as answering the question 'across what surface do you want to measure the flow of the quantity of the first vector?' (the second vector is the normal to the surface)