What is Stress-energy tensor: Definition and 98 Discussions

The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. This density and flux of energy and momentum are the sources of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity.

View More On Wikipedia.org
Recent contents Top users
  1. kmm

    I Stress-energy tensor and energy/momentum conservation clarification

    I've been working through Bernard Schutz's book on GR and have run into some confusion in chapter 4 problem 20 part b. In this chapter, the stress-energy tensor for a general fluid was introduced and was used to derive the general conservation law for energy/momentum, where we found that...
  2. G

    I Diagonal Matrix of Stress-Energy Tensor: Why?

    I came across a statement in《A First Course in General Relativity》:“The only matrix diagonal in all frames is a multiple of the identity：all its diagonal terms are equal.”Why?I don’t remember this conclusion in linear algebra.The preceding part of this sentence is:Viscosity is a force parallel...
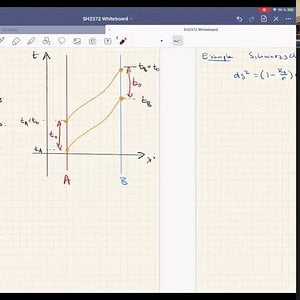
  3. SH2372 General Relativity - Lecture 7

    SH2372 General Relativity - Lecture 7

    0:00 Gravitational time dilation 12:06 Gravitational redshift 14:43 Dynamics of spacetime 34:17 Matter in spacetime 51:07 The stress-energy tensor 1:03:00 Ideal fluids
    • Orodruin
    • Media item
    • Gravitational redshift Gravitational time dilation Stress-energy tensor
    • Comments: 0
    • Category: Relativity
  4. G

    I Question about Stress-Energy Tensor: A First Course in GR

    I came across a statement in《A First Course in General Relativity》on page 97 which confused me.It read:"if the forces are perpendicular to the interfaces,then##T^i{^j}##will be zero unless ##i=j##". Where the ##T## is stress-energy tensor,##T^i{^j}##is the flux of i momentum across the j surface.
  5. ergospherical

    I Yang-Mills Stress-Energy Tensor Explained

    It's given as ##T_{\mu \nu} = - \mathrm{tr}(F_{\mu \lambda} {F_{\nu}}^{\lambda} - \frac{1}{4} g_{\mu \nu} F_{\alpha \beta} F^{\alpha \beta})##. Can somebody explain the notation, i.e. what is the meaning here of the trace? (usually I would interpret the trace of a matrix as the number...
  6. E

    B Understanding the Stress-Energy Tensor & Solar Mass in General Relativity

    In the test of General Relativity by perihelion motion of mercury, the stress-energy tensor is set to 0 in Schwarzschild solution. Then, is the curvature caused by solar mass, or by the 0 stress-energy? Or, do we consider solar mass as the gravitating mass? Or the 0 stress-energy the gravitating...
  7. Haorong Wu

    Stress-energy tensor for a rotating sphere

    The answer with no details is given by First, I considered a spherical shell because I thought the velocities at different radius ##r## will be different and hence the four-momentum will be different, as well. Then, I writed down the linear momenta by $$\epsilon^{ijk} r_i p_j = L_k$$ with...
  8. ohwilleke

    B Special Cases of Stress-Energy Tensor in GR

    Background and Motivation The stress energy tensor of general relativity, as conventionally defined, has sixteen components. One of those component, conventionally component T00, also called ρ, is mass-energy density, including the E=mc2 conversion for electromagnetic fields. The other...
  9. G

    I Variation of Metric and the Energy-Momentum Tensor: Where Am I Going Wrong?

    Given the action ##S =-\sum m_q \int \sqrt{g_{\mu\nu}[x_q(\lambda)]\dot{x}^\mu_q(\lambda)\dot{x}^\nu_q(\lambda)} d\lambda## The Energy-Momentum Tensor (EMT) is defined by the variation of the metric $$\delta S = \frac{1}{2}\int T_{\mu\nu} \delta g^{\mu\nu} \sqrt{g} d^4x$$ Then I use two...
  10. F

    I Understanding the Stress-Energy Tensor in Special Relativity

    Hello, I try to understand how to get the last relation below ##(3)## ( from stress energy tensor in special relativity - Wikipedia ). I understand how to get equation ##(1)## but I don't grasp how to make appear the gradient operator in the dot product and the divergence operator in the...
  11. Q

    A Can you numerically calculate the stress-energy tensor from the metric?

    About 10 years ago I worked on a project where I took a mater distribution and numerically solved for spatial curvature. Can this be done in the opposite direction? Can anybody point me to a resource that would allow me to calculate matter distributions when the metric is specified? What are...
  12. JD_PM

    A Understanding how to derive the stress-energy tensor formula

    Tong proposes the following exercise in this lecture (around 25:30, section b)): Exercise statement: Prove that the stress-energy tensor is given by the functional derivative of the action with respect to ##\delta g^{\mu \nu}## $$T_{\mu \nu} = \frac{-2}{\sqrt{-g}} \frac{\delta S}{\delta...
  13. JD_PM

    Prove the well-established (in GR) stress-energy tensor formula

    Prove that the stress-energy tensor is given by the functional derivative of the action with respect to ##\delta g^{\mu \nu}## $$T_{\mu \nu} = \frac{-2}{\sqrt{-g}} \frac{\delta S}{\delta g^{\mu \nu}}$$ Tong suggests (around 25:30) we could get the desired tensor by performing a...
  14. Ibix

    A Stress-energy tensor of a rotating rod

    A rod rotates freely (edit: about an axis perpendicular to its length) in empty space. Working in an inertial coordinate system where the rod rotates around a fixed point, the rod is straight, of length ##2L## in its spinning state, and its mass distribution is symmetric along its length. The...
  15. ohwilleke

    I How big are the non-mass parts of the stress-energy tensor?

    In Newtonian gravity, non-rest mass contributions to gravitational effects are ignored and for many purposes (e.g. low precision solar system astronomy, N-body approximations of galaxy or galaxy cluster dynamics), the other contributions that enter Einstein's field equations through the...
  16. Creedence

    I Eigenvectors of the EM stress-energy tensor

    My question is that what is the physical meaning of the EM stress-energy tensor's eigenvectors? Thanks for the answers - Robert
  17. sergiokapone

    I Covariant derivative of the contracted energy-momentum tensor of a particle

    The energy-momentum tensor of a free particle with mass ##m## moving along its worldline ##x^\mu (\tau )## is \begin{equation} T^{\mu\nu}(y^\sigma)=m\int d \tau \frac{\delta^{(4) }(y^\sigma-x^\sigma(\tau ))}{\sqrt{-g}}\frac{dx^\mu}{d\tau}\frac{dx^\nu}{d\tau}. \end{equation} Let contract...
  18. pixel

    I Stress-Energy Tensor: Specified or Calculated?

    My understanding is that this tensor contains sources for spacetime curvature, analogous to how charge and current are sources for electric and magnetic fields. In other words, the elements of this tensor, such as mass density, are specified and used in the Einstein equation to solve for the...
  19. H

    I Understanding the stress-energy tensor

    I have trouble understanding some terms in the stress-energy-tensor. For instance T^(12) stands for the flux of the x-component of momentum in the y-direction. But what does it means for the x-component of momentum to flow in the y direction? Since momentum is a vector should't the x-component...
  20. F

    I Get Relation from Stress-Energy Tensor Def.

    Starting from the following definition of stress-energy tensor for a perfect fluid in special relativity : $${\displaystyle T^{\mu \nu }=\left(\rho+{\frac {p}{c^{2}}}\right)\,v^{\mu }v^{\nu }-p\,\eta ^{\mu \nu }\,}\quad(1)$$ with ##v^{\nu}=\dfrac{\text{d}x^{\nu}}{\text{d}\tau}## and...
  21. T

    I How does the stress-energy tensor act on gravity?

    How do the components of the stress-energy tensor act on gravity regarding a) the FRW-universe? b) a solid ball? In a FRW-universe ##\rho + 3P## determines the second derivative of the scale factor. So, there are no non-diagonal components. Just theoretically, if the perfect fluid was...
  22. P

    A Compute Normal Forces on Box Sides via Stress-Energy Tensor

    Suppose one has a box moving through flat space-time with a stress energy tensor ##T^{ab}## that's non-zero inside the box and zero outside the box. How does one compute the normal forces on the faces of the box associated with it's motion? I am assuming that the normal forces are measured...
  23. sergiokapone

    I Stress–energy pseudotensor of gravitation field for DE

    Suppose we have Einstein equation for *Universe free of matter* in form \begin{equation} G_{ik} = \chi T_{ik}, \end{equation} where the cosmological constant $\Lambda$ is transferred to the RHS of equation and written in the form of stress–energy tensor of Dark Energy...
  24. V

    I Proving Effects of Stress-Energy Tensor on Curvature

    Hi everyone. Could you help me to find the way to prove some things? 1)Changing of body velocity or reference frame don't contribute to spacetime curvature 2)On the contrary the change of body mass causes the change of curvature in local spacetime I use the assumption that if we have the same...
  25. P

    A Exploring the Stress-Energy Tensor of a Perfect Fluid

    I believe this thread is sufficiently different from one that was recently closed to not violate any guidelines, though there are unfortunately some similarities as the closed thread sparked the questions in my mind. If we look at the stress energy tensor of a perfect fluid in geometric units...
  26. Amaterasu21

    I Getting Invariant Curvature from Momentum & Energy

    Hi all, I understand the mathematics behind special relativity pretty well, but I only have a bare conceptual understanding of general relativity. My understanding is that energy, momentum and stress (as described in the energy-stress tensor) are what contribute to space-time curvature and...
  27. X

    A Complex components of stress-energy tensor

    Hi All, I am evaluating the components of the stress-energy tensor for a (Klein-Gordon) complex scalar field. The ultimate aim is to use these in evolving the scalar field using the Klein-Gordon equations, coupled to Einstein's equations for evolving the geometric part. The tensor is given by...
  28. davidge

    I Finding Stress-Energy Tensor: General Rules & Variational Principle

    I wonder if there is a "general rule", a kind of "algorithm" for finding the components of the Stress-Energy tensor in for particular cases. For the Einstein tensor, just by knowing the metric, one can find the components of it. What about the Stress-Energy tensor? One way I thought of (and...
  29. Z

    A Two questions on the Stress-Energy Tensor

    I am trying to get a good feel for the Stress-Energy tensor, but I seem to be hung up on a few concepts and I was wondering if anyone could clear up the issues. First, when I look at the derivation of the Stress-Energy tensor for a perfect fluid (of one species, say), the 00 entry can be...
  30. S

    A Stress-Energy Tensor - derivation

    In page 64 of David Tong's notes (http://www.damtp.cam.ac.uk/user/tong/string/four.pdf) on conformal field theory, Tong mentions that 1. the stress-energy tensor is defined as the matrix of conserved currents which arise from translational invariance, $$\delta\sigma^{a} = \epsilon^{a},$$ where...
  31. S

    I Definition of stress-energy tensor

    Hello! Why is the stress energy tensor defined as a (2 0) tensor? I understand that it needs 2 one-forms as arguments, but using the metric, can't we bring it to (1 1) or (0 2)? So is there is any physical or mathematical reason why it is defined as (2 0), or it is equally right to define it as...
  32. e2m2a

    B Mass & Stress-Energy Tensor: Why Not Explicitly?

    Why doesn't mass show up in the stress-energy tensor explicitly?
  33. J

    A Stress-Energy Tensor: Basics & Questions

    I understand the basics of the stress-energy tensor (I think) but I still have a couple questions about it. But first, I'd like to give a quick run down of what I do understand, and I would appreciate if one of you could correct me where I am wrong and also answer my questions afterward. So...
  34. pixel

    I Calc Precession of Mercury Orbit: Stress-Energy Tensor=0?

    In the calculation of the precession of Mercury's orbit, why is the stress-energy tensor equal to 0? There is energy and momentum at the location of the planet.
  35. A

    What is the purpose of the Einstein stress-energy tensor?

    Hello I'm new here on this forum and on physics too. I have problem on Einstein famous equation I have a problem on the last component Tαβ I know that tensor name is Einstein stress-energy tensor and I know that Tαβ...
  36. T

    Static universe, spacetime and the stress-energy tensor

    Einstein's static universe obeys ##\rho = 2\lambda##. So, attractive and repelling gravity cancel each other. I'm curious about the spacetime in this universe. Because the scale factor is constant, it seems that neighboring co-moving test particles don't show relative acceleration, thus no...
  37. HeavyMetal

    Panda"Understand Relationship between Stress-Energy Tensor and Interval

    Hello all, I have a homework question that I am almost 100% sure that I solved, so I do not believe that this post should go into the "Homework Questions" section. This thread does not have to do with the answer to that homework question anyways, but rather a curiosity about whether or not this...
  38. I

    Heuristic Evaluation of Stress-Energy Tensor

    I've been reading through Schutz's A First Course in General Relativity, and my solution to a particular problem has got me wondering if I'm being careful enough in my approach. The problem states: Show that, in the rest frame ##\mathcal{O}## of a star of constant luminosity ##L## (total energy...
  39. M

    Stress-energy tensor as source of gravity

    Hello. This is a question for the philosophers. I know just a little bit about QT and GR, but have a solid background in QM, classical physics and some particle physics. I was wondering about the stress energy tensor. I know that the graviton must have spin 2 because the source of gravity is a...
  40. P

    Divergence of the Stress-Energy Tensor

    Im studying Quantum Field Theory as part of my undergraduate course, and am currently looking at Noether's Theorem which has led me to the following calculation of the divergence of the Stress-Energy Tensor. I'm having difficulty in seeing how we get from line (31) to line (32). Is the 2nd term...
  41. M

    Conservation of Stress-Energy tensor

    I have a few questions regarding the solution to this problem. First of all I have the Stress-Energy tensor for a scalar fields \phi^a T_{Noether}^{\mu\nu} = \displaystyle \sum_a \frac{\partial \mathcal{L}}{(\partial_{\mu}\phi_a)}\partial^{\nu}\phi^a - g^{\mu \nu}\mathcal{L} To ensure...
  42. A

    How to derive Maxwell stress-energy tensor

    The problem statement is: Assuming that we are in vacuum, and that the only work done between mechanical systems and electricity and magnetism comes from the Lorentz force, give a full, relativistic derivation of the Maxwell stress-energy tensor.
  43. S

    1st stress-energy tensor component for an electric field

    I have recently gone over the derivation of the stress energy momentum tensor elements for the special case of dust. This case just used a swarm of particles. Now that I understand that case, I am now trying to see if I can derive the components for an electric field. I just want you guys to...
  44. I

    Exotic stress-energy tensor and causality

    Hello everybody. I would like to kindly ask your help with a hypothetical hairy question about which I think a lot recently. It is known fact, that it is not possible to construct a wormhole without exotic mass that violates the weak energy condition. It is also known that many quantum fields...
  45. bcrowell

    Parity of stress tensor versus stress-energy tensor

    The stress-energy tensor is an actual tensor, i.e., under a spacetime parity transformation it stays the same, which is what a tensor with two indices is supposed to do according to the tensor transformation law. This also makes sense because in the Einstein field equations, the stress-energy...
  46. C

    Stress-energy tensor explicitly in terms of the metric tensor

    I am trying to write the Einstein field equations $$R_{\mu\nu}-\frac{1}{2}g_{\mu\nu} R=\frac{8\pi G}{c^4}T_{\mu\nu}$$ in such a way that the Ricci curvature tensor $$R_{\mu\nu}$$ and scalar curvature $$R$$ are replaced with an explicit expression involving the metric tensor $$g_{\mu\nu}$$...
  47. D

    Why is the stress-energy tensor symmetric?

    If we use the "flux of 4-momentum" definition of the stress-energy tensor, it's not clear to me why it should be symmetric. Ie, why should ##T^{01}## (the flux of energy in the x-direction) be equal to ##T^{10}## (the flux of the x-component of momentum in the time direction)?
  48. S

    Stress-energy tensor for a single photon

    Hi, I'm trying to write down the stress-energy tensor for a single photon in GR, but I'm running into trouble with its transformation properties. I'll demonstrate what I do quickly and then illustrate the problem. Given a photon with wavevector p, we write {\bf T} = \int \frac{\mathrm{d}^3...
  49. bcrowell

    Maxwell's equations from divergence of stress-energy tensor?

    If I start with the stress-energy tensor T^{\mu\nu} of the electromagnetic field and then apply energy-momentum conservation \partial_\mu T^{\mu\nu}=0, I get a whole bunch of messy stuff, but, e.g., with \nu=x part of it looks like -E_x \nabla\cdot E, which would vanish according to Maxwell's...
  50. D

    What is the Lorentz invariance of flux in the stress-energy tensor?

    According to Wikipedia, This definition doesn't sit well with me. Flux is defined as the rate that something passes through an infinitesimal surface, divided by the infinitesimal area of that surface. For example, the current flux (or current density), when dotted with a unit vector, gives...
Back
Top