Discussion Overview
The discussion revolves around calculating the visible curvature of the horizon from various altitudes, exploring the mathematical treatment of this phenomenon and its potential publication in a scientific journal. Participants share insights on the nature of the horizon's curvature and its measurement, as well as the implications of altitude on visibility.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant is writing a paper on calculating the visible curvature of the horizon and seeks publication advice.
- Another participant notes that the journal choice depends on the application of the solution and suggests conducting a literature search.
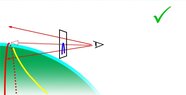
- There is a discussion about the angular depression of the horizon increasing with altitude, which can be measured with a theodolite.
- Some participants question how to define "curvature of the horizon," suggesting it is always circular and can be measured as an angle from the vertical.
- A participant clarifies that their paper focuses on how the horizon appears curved from different altitudes, contrasting this with the straight line appearance at sea level.
- Concerns are raised about the novelty of the work if the author does not reference existing literature.
- Another participant challenges the complexity of the calculations, suggesting they may be basic trigonometry.
- There is a distinction made between calculating the distance to the horizon and calculating the curved shape of the horizon as perceived by an observer.
- One participant inquires whether the calculations are based on a spherical Earth or an oblate spheroid, noting that the latter would add complexity.
- Another participant discusses the implications of atmospheric refraction on horizon calculations and the need for something novel to be published.
- The author states they are calculating for a spherical Earth, believing that the visual differences would be negligible.
- There is a debate about the interpretation of curvature and how it appears to an observer at different altitudes.
Areas of Agreement / Disagreement
Participants express differing views on the novelty and complexity of the calculations involved in determining the curvature of the horizon. There is no consensus on the publication potential or the mathematical treatment of the problem, with multiple competing perspectives remaining.
Contextual Notes
Some participants highlight limitations regarding the lack of references and potential rediscovery of existing knowledge. The discussion also touches on the effects of atmospheric refraction, which complicates the calculations.