What is the relationship between friction and momentum?

[pinsky]

I've been breaking my head a couple of hours to figure out the concept of momentum, and it's difference between kinetic energy. Here's what i came up with, please correct the things which are wrong.

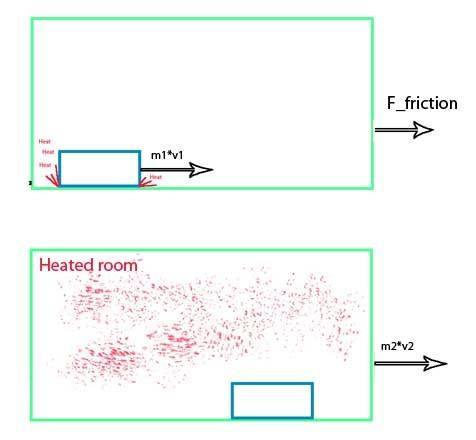
The blue object has a starting velocity v_1 so it has a momentum v_1 \cdot m_1[\tex].<br /> <br /> The green rectangle represents a closed system. <br /> <br /> As the blue object moves, it looses its kinetic energy do to friction, and at the same time it transfers the momentum to the system. Since there is a force on both the blue and the green rectangle, each of them is accelerating in the direction of the force.<br /> <br /> When all the kinetic energy is converted to heat, the blue object stops, and at that same time, all of the momentum has been transferred to the green rectangle.<br /> <br /> <br /> Just one thing, to avoid confusion. I am aware that I can&#039;t say that <blockquote data-attributes="" data-quote="" data-source="" class="bbCodeBlock bbCodeBlock--expandable bbCodeBlock--quote js-expandWatch"> <div class="bbCodeBlock-content"> <div class="bbCodeBlock-expandContent js-expandContent "> Since there is a force on both the blue and the green rectangle, each of them is accelerating in the direction of the force. </div> </div> </blockquote> because it would be normal that i observe the relative movement of the green object compared to the STATIC blue rectangle (because i defined it as the closed system).<br /> I did so on purpose. While trying to figure out the relationship between friction and momentum <br /> <blockquote data-attributes="" data-quote="" data-source="" class="bbCodeBlock bbCodeBlock--expandable bbCodeBlock--quote js-expandWatch"> <div class="bbCodeBlock-content"> <div class="bbCodeBlock-expandContent js-expandContent "> why was there a conservation of momentum if i loose speed do to friction? </div> </div> </blockquote>i tried observing a calculator on my desk.<br /> <br /> I push my calculator, it moves a bit and then stops do to friction. I couldn&#039;t see where the movement went because i considered my table the closed system and it didn&#039;t move when i pushed my calculator (at least not enough for me to notice :) ). <br /> If I could notice, i would see that the table transfer its momentum to the house floor, which transfers its momentum to the planet earth. <br /> <br /> I hope you understand why i called the green rectangle a closed system, and then observed he whole drawing from a even larger perspective. To me, limiting myself to a closed system (in the real meaning of that word) was the main problem of failing to understand momentum.<br /> <br /> <br /> This leads me to another conclusion.<br /> <br /> The kinetic energy of a moving object can&#039;t all be converted to heat (or sound) but must also partially be transferred to a different object in kinetic energy form.<br /> I think there must be a formula which defines how much of the energy must remain kinetic.

 

[Matterwave]

That second arrow should be to the right. Conservation of momentum is not just conservation of the magnitude of momentum, but the direction also. If the blue block was initially moving to the right, then at the end when it's stopped with respect to the green box, the entire system must be moving to the right (albeit slower).

The force on the blue block is to the left, tending to slow it down; however the force on the green box, by Newton's third law, must be to the right (equal and opposite).

Indeed not all of the kinetic energy can be converted into heat, some of it must remain with the final system. How much kinetic energy is left can be calculated using conservation of momentum. (You'd hafta know the mass of the green block as well as the blue block).

 

[A.T.]

This leads me to another conclusion.
The kinetic energy of a moving object can't all be converted to heat (or sound) but must also partially be transferred to a different object in kinetic energy form.

Only if the total momentum of the two objects is not zero. Think of two identical masses colliding head-on with the same velocities, and sicking together after that: All KE is gone.

 

[pinsky]

Tnx for the quick replays, I've fixed the mistake.

I have another question dough.

Let's say I'm holding a ball still in my hands. At that moment the momentum is 0 since the ball isn't moving.

When I let the ball go, it starts falling so it gains speed. It's mass is unchanged so now the momentum isn't zero anymore.

How to explain that?

 

[A.T.]

Let's say I'm holding a ball still in my hands. At that moment the momentum is 0 since the ball isn't moving.

When I let the ball go, it starts falling so it gains speed. It's mass is unchanged so now the momentum isn't zero anymore.

It is still zero, because the Earth also starts falling towards the ball. The reference frame of the Earth is only approximately inertial.

 

[Naty1]

Have you read about INERTIA?

http://en.wikipedia.org/wiki/Inertia

...an object that is not subject to any net external force moves at a constant velocity. In even simpler terms, inertia means that an object will always continue moving at its current speed and in its current direction until some force causes its speed or direction to change. This would include an object that is not in motion (velocity = zero), which will remain at rest until some force causes it to move.

 

[pinsky]

Have you read about INERTIA?

http://en.wikipedia.org/wiki/Inertia

To what part of the discussion are you referring?

 

[Matterwave]

Tnx for the quick replays, I've fixed the mistake.

I have another question dough.

Let's say I'm holding a ball still in my hands. At that moment the momentum is 0 since the ball isn't moving.

When I let the ball go, it starts falling so it gains speed. It's mass is unchanged so now the momentum isn't zero anymore.

How to explain that?

There are 2 ways to explain this. 1) Momentum is only conserved in the absence of external forces. The external force of Earth's gravity means the momentum of the ball is not conserved. 2) As A.T. mentioned, you can internalize the force of gravity by including the Earth in your system as well. In this case, the Earth "falls" towards the ball to preserve momentum; however, this movement is so small that it is completely dwarfed by all other effects.