What Is the Speed of a Point on a Car Tire in Motion?

[scoutfai]

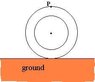
The question is : The speed of a car traveling on a straight horizontal road is V. What is the speed of the point P on the tyre of the car ?

(A) 0.5V (B) V (C) 2V (D) 3V


i got try to solve it myself, and i get the answer (B)...
However, my teacher do it and get answer (C)...
i am not confidence with my method, but i also not agree with (or i should say i don't understand what he doing) my teacher method..
i will show both methods mentioned above, i hope any expert can give me a better explanation and calculation. U help is meaningful to me !

My method :
Since the speed of the car is V, hence the speed of the centre of the wheel is also V.
let the speed of the point P be X, now we should find X in term of V.
X = linear velocity of point P
X = rw where r = radius of wheel and w = angular velocity of the wheel
we know w = 2(pi) / T , this mean in time T, the wheel make one complete revolution.
In time T also, the wheel move horizontally with distance 2(pi)r
since speed = distance / time, hence V = 2(pi)r / T
thus T = 2(pi)r / V
therefore w = 2(pi) / T
= 2 (pi) / {2(pi)r / V }
= 2V(pi) / [2r(pi)]
= V / r
so X = rw = r ( V/r )
X = V
Do u agree with my method ? if not, please tell me why !

My teacher method is :
from the diagram, let the centre of the wheel be O and the line joining the point P and O will intercept with the point on the ground ( the tangential point of the wheel surface to the ground ) where the wheel touch the ground.
so, let this point called as Q.
the distance QO = r
distance QP = 2r
from V = rw where v = linear velocity, r = radius of the body , w = angular velocity, hence V is direct proportional to r
so V / r = constant
so { V / r for point O } = { V / r for point P }
if the V of P = x, then x / 2r = V / r
x = (v/r)(2r)
x = 2v
do u agree with my teacher method ? if you say yes, please explain to me why my teacher can use the point Q as the point of axis of rotation of the wheel. If you say no, tell me your reason also. Thanks you, u help is meaningful to me.

 

[arildno]

Welcome to PF!
Unfortunately, I cannot open your attachment, however I think I can help you out:
Your teacher is right:

First, I'll say what I think your diagram shows:
Your point P is at the top of the wheel, point O is the center, point Q is at the bottom( in contact with the ground), while the car moves with velocity V (am I right?)

You state: X=rw
This is completely wrong.
rw is the rate by which P moves relative to O (think about it)
Hence, since rw is only P's relative velocity to O, X must be the sum of O's velocity and rw:
X=V+rw
This argument agrees with your teacher's

 

[scoutfai]

i can understand what you try to say.
If like this, i try to change the question a bit. Let say now we have a point Y on the wheel with some angle T to the line POQ (either clockwise direction or anticlockwise direction ), then what is the speed of the point Y on the tyre of the car ?

 

[Doc Al]

Let say now we have a point Y on the wheel with some angle T to the line POQ (either clockwise direction or anticlockwise direction ), then what is the speed of the point Y on the tyre of the car ?

Use the same logic as arildno explained, only now you must treat the velocities as vectors since they won't be going in the same direction. Let "y" represent the point on the wheel, "g" represent the ground, and "c" represent the center of the wheel.
\vec{V_{y/g}} = \vec{V_{y/c}} + \vec{V_{c/g}}

\vec{V_{c/g}} is just the velocity of the center of the wheel with respect to (wrt) the ground: V m/s in the x-direction.

\vec{V_{y/c}} is just the velocity of y wrt the center of the wheel: V m/s in a direction tangent to the wheel.

So, depending upon where "y" is along the wheel, its speed wrt the ground can be anywhere from 0 to 2V. If it is at an angle of \theta (clockwise) from vertical, \vec{V_{y/c}} would have an x-component of V cos\theta and a y-component of -V sin\theta.